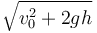No Boletín - Otro tiro parabólico (Ex.Sep/15)
De Laplace
Revisión a fecha de 15:15 1 mar 2016; Enrique (Discusión | contribuciones)
1 Enunciado
Un proyectil se mueve en el plano vertical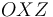 
. Se conoce su aceleración constante (debida a su propio peso), y también su posición y su velocidad en el instante inicial (
):
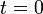![\vec{a}(t)=-g\,\vec{k}\,\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\vec{r}(0)=h\,\vec{k}\,\,\,;
\,\,\,\,\,\,\,\,\,\,\,\,\vec{v}(0)=v_0\,[\,\mathrm{cos}(\theta)\,\vec{\imath}+
\mathrm{sen}(\theta)\,\vec{k}\,]](/wiki/images/math/d/e/9/de9c3ce06bffd9ab7a69070c76c7c6b8.png)
donde 
, 
y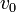 
tienen valores positivos, y 
está comprendido en el intervalo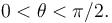 
- Determine el radio de curvatura de la trayectoria del proyectil en el instante inicial.
- Determine la celeridad del proyectil en el instante en el que su trayectoria corta al eje
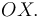
2 Radio de curvatura en el instante inicial
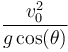
3 Celeridad del proyectil al cortar el eje OX
