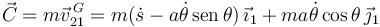Barra con muelle horizontal, Febrero 2016 (MR G.I.C.)
De Laplace
1 Enunciado
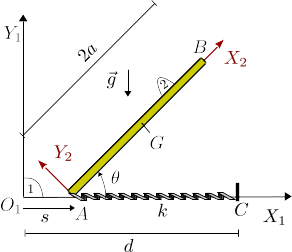
Una barra de longitud 2a y masa m (sólido "2") desliza con un extremo (punto A) apoyado sobre un plano horizontal liso. El extremo A está unido a un muelle de constante elástica k y longitud natural nula anclado en C que se mantiene siempre horizontal. La gravedad actúa verticalmente hacia abajo. En t = 0 la barra estaba en reposo, el punto A coincidía con O1 y la barra estaba completamente vertical.
- Encuentra la expresión que da la cantidad de movimiento de la barra.
- Encuentra la expresión que da el momento cinético de la barra respecto del punto A.
- Determina las ecuaciones de movimiento del sistema.
- ¿Cómo es la fuerza de ligadura en el punto A?
- Supongamos que se fuerza al punto A a moverse con velocidad uniforme
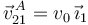 . ¿Cual de estas fuerzas aplicadas en A consigue ese efecto?
. ¿Cual de estas fuerzas aplicadas en A consigue ese efecto?
2 Solución
2.1 Cinemática de la barra
Vamos a determinar la reducción cinemática de la barra. Al ser un movimiento plano, y dado que el eje X2 forma un ángulo θ con el eje fijo X1, el vector rotación es
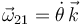
Por otro lado, la velocidad absoluta del punto A de la barra es
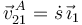
Ahora calculamos la velocidad en el centro de masas de la barra
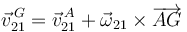
Como
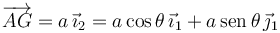
tenemos
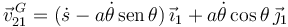
y la cantidad de movimiento de la barra es