Equilibrio mecánico y térmico. Presión y temperatura (GIE)

De Laplace

Revisión a fecha de 18:50 14 feb 2016; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Presión
2 Sistemas en equilibrio mecánico
3 Principio cero de la termodinámica
- 3.1 Equilibrio térmico
- 3.2 Principio cero de la termodinámica
4 Medida de la temperatura

1 Presión

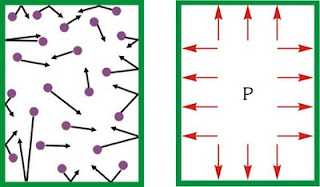
Supongamos que tenemos un cilindro lleno de un gas y que la tapa de este cilindro es un pistón que puede deslizarse sin rozamiento. Supongamos también que en el exterior del cilindro existe el vacío absoluto. En ese caso sabemos lo que ocurrirá: el gas del interior del cilindro se expandirá, desplazando al pistón (de forma más o menos acelerada, según la masa del pistón).

El mecanismo por el que esto ocurre son las colisiones de las moléculas de gas con el pistón. En cada colisión, supuesta elástica, la partícula experimenta un cambio en su cantidad de movimiento, que es ganado por el pistón.

Por tanto, para mantener el pistón en su lugar, es preciso ejercer una fuerza externa sobre él en la dirección normal a su movimiento. La fuerza necesaria será mayor cuanto mayor sea el área del pistón, por lo que la fuerza externa que hay que aplicar es de la forma

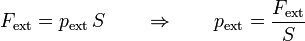
$F_\mathrm{ext} = p_\mathrm{ext}\,S\qquad\Rightarrow\qquad p_\mathrm{ext}=\frac{F_\mathrm{ext}}{S}$

siendo $p ext$ la fuerza aplicada por unidad de superficie. A esta cantidad se la denomina presión.

Si conseguimos que el pistón se quede en equilibrio, llegamos a la conclusión de que la fuerza por unidad de superficie ejercida por el gas es igual a la aplicada desde fuera y por tanto el gas posee una presión

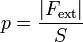
$p = \frac{|F_\mathrm{ext}|}{S}$

Hemos definido la presión en términos de la fuerza aplicada desde fuera porque ésta es la que medimos fácilmente, si bien en estados de equilibrio, que son los que nos interesarán principalmente, podremos hablar igualmente de la fuerza aplicada desde el interior.

La presión de un gas no es una magnitud dependiente de la superficie del gas, aunque sea ahí donde se mida. Es una propiedad de todo el gas. Para verlo, imaginemos que en una cámara llena de un gas introducimos una lámina que la separa en dos partes. En cada una de sus caras seguirán produciéndose esas colisiones moleculares, si bien en promedio habrá tantas a un lado como al otro y la lámina permanecerá en equilibrio.

En una muestra de gas de tamaño reducido, todo el gas se encuentra a la misma presión y cualquier aumento en la presión en un punto se transmite a todos los puntos de la muestra (principio de Pascal).

En una muestra de gas de gran tamaño la presión podrá variar de un punto a otro, incluso estando en equilibrio.

En el caso de un fluido (gas o líquido), de densidad uniforme, la presión va aumentando con la profundidad, ya que cuanto más profundo mayor es el peso de la columna de líquido.

Supongamos que tenemos una columna de líquido de altura $h$ respecto a una posición $z = 0$ . Por encima de la cual se ejerce una presión $p 0$ . En este caso, la fuerza normal ejercida en $z = 0$ es

$F = mg + p_0S = \rho S h g + p_0 S\,$

y por tanto la presión en este punto es

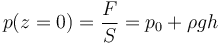
$p(z=0) =\frac{F}{S}=p_0+\rho g h$

El segundo término, conocido como presión hidrostática y es importante en el caso de los líquidos. Así, para el caso del agua, una columna de aproximadamente 10m añade una presión equivalente a una atmósfera.

A modo de ejemplo, consideremos un barómetro elemental formado por un tubo en U de sección constante $S$ que contiene un líquido de densidad $ρ 0$ . Uno de los brazos está cerrado, mientras que el otro está abierto al exterior. Cuando la presion exterior es $p 0$ , los dos niveles está a la misma altura. Si ahora disminuye la presión exterior, el aire del brazo cerrado empuja al líquido y se produce un desnivel, que podemos medir. Imaginemos que la longitud inicial de la cámara es $h 0$ y el desnivel es $Δ h$ . En ese caso, los puntos A y B, situados a la misma altura, tienen la misma presión

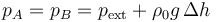
$p_A=p_B=p_\mathrm{ext}+\rho_0g\,\Delta h$

Por otro lado, si el gas de la cámara es ideal cumple la ley de Boyle

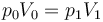
$p_0V_0=p_1V_1\,$

que en este caso da

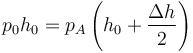
$p_0h_0=p_A\left(h_0+\frac{\Delta h}{2}\right)$

y por tanto

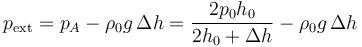
$p_\mathrm{ext}=p_A-\rho_0g\,\Delta h = \frac{2p_0h_0}{2h_0+\Delta h}-\rho_0 g\,\Delta h$

En un gas este efecto es mucho menos apreciable y para volúmenes pequeños puede suponerse que la presión es homogénea.

A la hora de estudiar la presión atmosférica el cálculo debe considerar que la densidad disminuye con la altura, por lo que el peso de la columna debe hallarse mediante una integral.

De la definición de presión se deduce que se mide en el SI en N/m². A esta unidad se la denomina pascal (Pa)

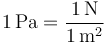
$1\,\mathrm{Pa} = \frac{1\,\mathrm{N}}{1\,\mathrm{m}^2}$

Un pascal es una unidad muy pequeña (es aproximadamente la presión que ejerce un folio situado horizontalmente sobre una mesa), por lo que se suelen usar múltiplos.

En las centrales térmicas la presión a la que se encuentra el vapor es de varios megapascales (1 MPa = 10⁶Pa), por lo que esta unidad es de uso frecuente.

Así, un bar equivale a

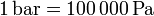
$1\,\mathrm{bar}= 100\,000\,\mathrm{Pa}$

y un milibar será

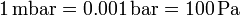
$1\,\mathrm{mbar}= 0.001\,\mathrm{bar}=100\,\mathrm{Pa}$

El bar y el milibar son unidades en desuso, en su lugar usaremos combinaciones de kilopascales y megapascales. En los pronósticos meteorológicos, al milibar se lo denomina actualmente hectopascal.

Por desgracia, están aun en uso diversas unidades que no pertenecen al SI: la atmósfera estándar

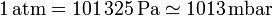
$1\,\mathrm{atm}=101\,325\,\mathrm{Pa} \simeq 1013\,\mathrm{mbar}$

el milímetro de mercurio o torr

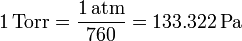
$1\,\mathrm{Torr} = \frac{1\,\mathrm{atm}}{760}= 133.322\,\mathrm{Pa}$

el psi (libra por pulgada cuadrada), habitual en la maquinaria anglosajona

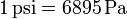
$1\,\mathrm{psi}=6895\,\mathrm{Pa}$

la atmósfera técnica, igual al peso de un kilogramo por centímetro cuadrado

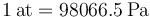
$1\,\mathrm{at}= 98066.5\,\mathrm{Pa}$

A la hora de medir la presión, hay dos conceptos que conviene no confundir.

Presión absoluta: es la que se mide respecto a una presión nula, $p$
Presión manométrica: es la que se mide respecto a la presión atmosférica

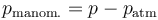
$p_\mathrm{manom.} = p - p_\mathrm{atm}\,$

La razón de la distinción es que la presión de un gas, como el que llena un neumático, se mide con un manómetro, que se basa en la fuerza debida a la diferencia de presiones entre la presión del gas y la exterior, que suele ser la atmosférica. Por ello, al llenar un neumático con una presión de “2.1” hay que saber primero que la unidad es el bar (que es casi una atmósfera estándar) y segundo que la presión es manométrica, por lo que la presión absoluta del aire del neumático sería 3.1 bares.

La diferencia entre manómetro y barómetro es que este último se usa para medir presiones atmosféricas, por lo que ya viene graduado en presiones absolutas (aunque internamente funcione como cualquier otro manómetro).

2 Sistemas en equilibrio mecánico

Para enunciar el principio cero de la termodinámica, referido al equilibrio térmico entre sistemas, conviene establecer en primer lugar una analogía con el equilibrio mecánico.

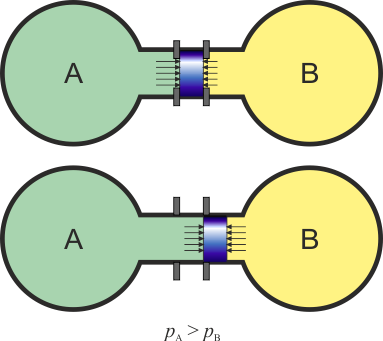
Consideremos dos tanques de gas conteniendo volúmenes de aire a presiones que pueden ser iguales o diferentes. Estos dos tanques se encuentran unidos por un cilindro, en el interior del cual se encuentra un pistón que puede deslizarse a lo largo del tubo. Inicialmente el pistón está sujeto externamente con una llave. En un momento dado se libera el pistón.

Si, al liberar el pistón, este comienza a desplazarse, llegamos a la conclusión de que las presiones de los gases a ambos lados son diferentes. No sabemos cuánto valen ni las presiones ni su diferencia, sólo que no son iguales.

Si, por el contrario, al liberar el pistón, este se queda en el mismo sitio, llegamos a la conclusión de que la presión a ambos lados es la misma, aunque no sabemos cuánto vale. En ese caso los dos tanque están en equilibrio mecánico.

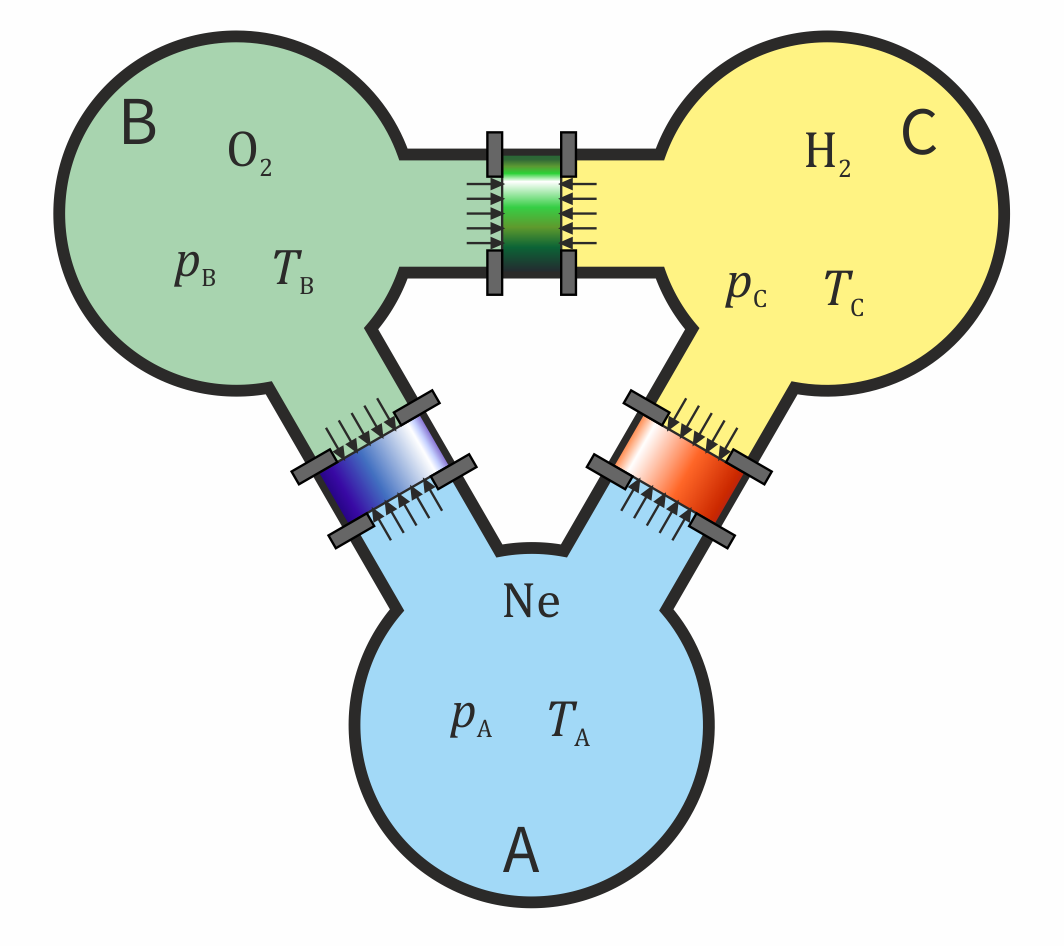
Consideremos ahora un caso en el que tenemos un sistema de tres tanques, A, B y C, que están conectados dos a dos por sendos tubos cilíndricos. Supongamos que liberamos el émbolo del tubo que conecta a A y a B y se queda en el sitio en que estaba. Ahora liberamos el que separa a A y a C y resulta que también permanece en el sitio. Sabemos lo que ocurrirá si liberamos el situado entre B y C: tampoco se moverá. La presión en B será la misma que en A y la de C también es la misma que la de A. Por tanto, las presiones de B y C son iguales y se encuentran en equilibrio mecánico. La liberación del pistón no supone cambio alguno, pues las fuerzas a ambos lados son de la misma magnitud.

Diremos entonces que "dos volúmenes de gas en equilibrio mecánico con un tercero, están en equilibrio mecánico entre sí". Y podremos afirmar que los tres volumenes tienen una propiedad en común, que es la presión.

No todos los equilibrios cumplen esta propiedad transitiva. Supongamos que el tanque A contiene neón, el B contiene oxígeno y el C contiene hidrógeno. Si se abre el tubo que une a A y a B no se produce reacción química entre el oxígeno y el neón (que es un gas noble), los dos gases están en equilibrio químico. Si ahora abrimos el tubo que A y a C tampoco se produce reacción. El hidrógeno también se encuentra en equilibrio químico con el neón. Pero si ahora abrimos el tubo que conecta a B y a C, poniendo en contacto el oxígeno con el hidrógeno, sí que reaccionarán de manera bastante explosiva. El oxígeno y el hidrógeno no se encuentran en equilibrio químico.

3 Principio cero de la termodinámica

3.1 Equilibrio térmico

El estado de un sistema puede describirse por una serie de propiedades. A partir de la experiencia, consideramos que una de estas propiedades es la temperatura del sistema. Aun no hemos dado una definición precisa del término, pero entendemos que un sistema puede encontrarse a diferentes temperaturas. Así, a la presión atmosférica, un recipiente con agua tiene mayor temperatura que si contiene un bloque de hielo. De la experiencia tomamos conceptos como “caliente”, “templado” o “frío”. Se trata de definir de forma precisa el concepto de temperatura y construir una escala que permita medirla.

Por ejemplo, podemos poner en contacto un tubo lleno de mercurio con una tanque de gas. El estado del mercurio se define por la longitud que alcanza dentro del tubo, mientras que el del gas por la presión que mide un manómetro.

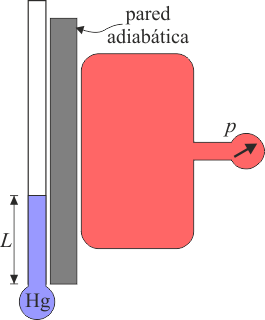
Un sistema está aislado térmicamente cuando, sea lo que sea lo que se pone en contacto con él, el estado del sistema no cambia. Esto se consigue rodeándolo de una pared aislante, como la de un termo. Una pared de este tipo se denomina una frontera adiabática.

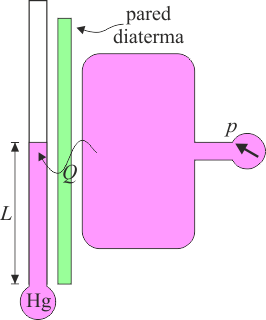
Si retiramos el aislamiento térmico, es posible que el estado de cada sistema cambie: el nivel del mercurio sube y la presión del gas baja. Concluimos que “algo” ha pasado de un sistema al otro, aunque no se ha realizado fuerza alguna sobre ellos. A ese “algo” se lo denomina calor (que aún no hemos definido de forma precisa). Normalmente, al poner en contacto dos sistemas, el calor sí puede fluir de un sistema al otro. En este caso, se dice que la frontera es diaterma o diatérmica.

Cuando ponemos en contacto dos sistemas mediante una pared diaterma y los sistemas no modifican su estado, pudiendo hacerlo, decimos que los dos sistemas se encuentran en equilibrio térmico. Es el análogo de que no se mueva el émbolo al conectar dos bombonas de gas.

3.2 Principio cero de la termodinámica

Estamos en condiciones de enunciar la primera de las leyes de la termodinámica. Supongamos que tenemos tres sistemas A, B, y C, como pueden ser los tres tanques de gas de la figura anterior. Se conectan los sistemas A y B a través de una pared diaterma y se comprueba que se encuentran en equilibrio térmico. Se conectan entonces el A y el C y se verifica que también se encuentran en equilibrio térmico. En ese caso, todas las experiencias muestran que si se conectan térmicamente los sistemas B y C tampoco cambiará su estado, esto es:

Principio cero de la termodinámica: Dos sistemas en equilibrio térmico con un tercero, se encuentran en equilibrio térmico entre sí.

Esta es una ley empírica que carece de demostración. Podemos considerarla razonable, por analogía con el caso del equilibrio mecánico, pero podría no cumplirse (como ocurre con el equilibrio químico, en el que no se cumple la propiedad transitiva).

Su extraño nombre se debe a que fue formulado como ley independiente en 1935 por Fowler, mucho después de que fueran enunciados el primer y el segundo principio de la termodinámica, pese a que lógicamente debe establecerse como condición previa.

4 Medida de la temperatura

4.1 Termómetros

El principio cero de la termodinámica nos permite definir la temperatura como “lo que miden los termómetros”. Esta definición parece demasiado simple y un tanto circular, pero es efectiva. La clave es que el principio cero nos permite construir un termómetro y una escala de temperatura. La forma de hacerlo es caracterizando cada valor de la temperatura por el valor correspondiente de otra propiedad del sistema (lo que se denomina una propiedad termométrica).

Supongamos que tenemos un sistema T consistente, por ejemplo, en un fino tubo de vidrio en cuyo interior existe una columna de mercurio. La altura de esta columna puede variar según el mercurio se dilate o contraiga. Si ahora colocamos este sistema T en contacto con un sistema A (un baño de agua, por ejemplo) el mercurio llega a una cierta altura; si acto seguido lo colocamos en contacto con otro sistema B y el mercurio llega a la misma altura que antes, llegamos a la conclusión de que A y B se encuentran en equilibrio térmico y les podemos asociar el mismo valor de la temperatura, siendo este valor, con las unidades adecuadas, la altura de la columna de mercurio.

La forma de construir un termómetro es entonces elegir un sistema caracterizado por una sola propiedad (la altura del mercurio, la presión de un gas, la dilatación de un metal, la diferencia de potencial entre dos electrodos, por ejemplo), asignar un valor de 0° a un valor determinado de esta propiedad y definir un “tamaño” del grado a partir de la variación de la propiedad entre dos puntos.

4.2 Escalas de temperatura

Para definir una escala de temperaturas hacen falta entonces un mínimo de dos puntos. Según los que se elijan se obtiene una escala u otra.

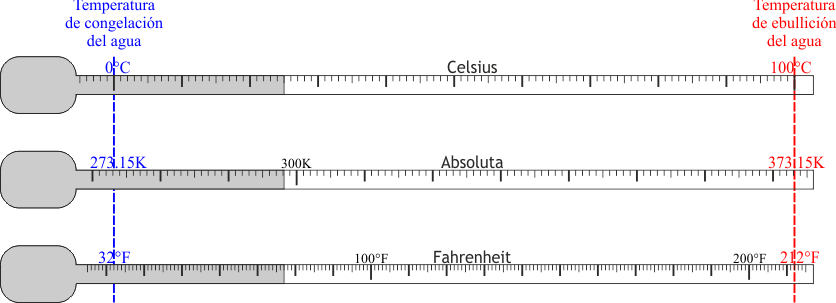
Escala Celsius: Se tomó como 0 °C (grados Celsius, también llamado grados centígrados) la temperatura de congelación del hielo a 1 atm de presión (101325 Pa) y como 100°C la de ebullición del agua a la misma presión.

Escala Fahrenheit: Definida originalmente como una que iba con el 0°F a la temperatura más baja a la que se podía conseguir agua líquida con sal y con 96°F a la temperatura “de un hombre sano”. Para evitar imprecisiones, hoy se define como que la temperatura de congelación del agua a 1 atm es 32°F y la de ebullición 212°F. Esto da la relación

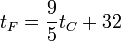
$t_F = \frac{9}{5} t_C +32$

Escala absoluta: Se establece como una escala que tiene su 0 K (kelvins, sin el “grado”) en el cero absoluto y tiene un valor de 273.16 K en el punto triple del agua (en el cual el agua líquida se encuentra en equilibrio térmico con el hielo y con el vapor de agua). En la práctica esto implica que los kelvins tienen el mismo tamaño que los grados Celsius y que la temperatura de congelación del agua a 1 atm es de 273.15 K, de forma que

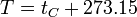
$T = t_C + 273.15 \,$

De hecho, hoy día se define la escala Celsius con esta relación, es decir, a partir de la temperatura absoluta. Por ello, hoy día, la temperatura de ebullición a 1 atm no es 100°C, sino 99.98°C.

Una consecuencia importante de que los kelvins tengan el mismo tamaño que los grados Celsius es que un incremento de temperaturas tiene el mismo valor en las dos escalas

$\Delta T = \Delta t_C\,$

Aparte de estas escalas existen otras como la Rankine (equivalente a la absoluta, pero con grados del tamaño de los grados Fahrenheit).

4.3 Temperatura absoluta

El problema que tiene la definición de temperatura basadas en las medidas de un termómetro concreto es que las escalas de los diferentes aparatos coincidirán en los dos puntos de referencia (a 0°C y 100°C en el caso de los grados Celsius), pero no tienen por qué coincidir en el resto de las temperaturas. Para una temperatura intermedia en la que el mercurio marca 50°C, quizás el termómetro de gas marca 50.01°C. Por ello, interesa definir una escala de temperaturas absoluta, que sea independiente del aparato de medida. Para hacer esto de forma rigurosa se necesita el segundo principio de la termodinámica, si bien se puede construir una escala con un termómetro de gas que se aproxima idealmente a la absoluta.

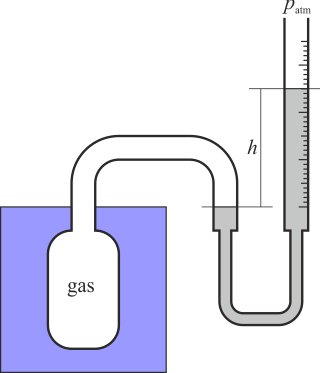
Para ello se emplea el termómetro de gas a volumen constante. Éste consiste esencialmente en una vasija que contiene un gas a baja presión. Esta vasija está conectada a un tubo flexible que contiene mercurio. El tubo flexible está unido a uno rígido abierto al exterior (a la presión atmosférica).

La vasija se pone en contacto con el líquido cuya temperatura se quiere medir. Si al variar la temperatura del gas éste se expande, variando su volumen, para mantener constante el volumen se eleva o baja el tubo rígido, de forma que aumenta la presión sobre el gas, comprimiéndolo hasta que vuelve a ocupar el volumen original. Cuando se ha alcanzado la posición original, se mide el desnivel entre dos tubos. Esto nos dice que la presión del gas es

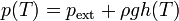
$p(T) = p_\mathrm{ext}+\rho g h(T)\,$

( $h$ puede ser negativa, si el gas está a una presión menor que la atmosférica). De esta forma podemos medir la temperatura a partir de la presión del gas, que a su vez se calcula mediante la lectura del nivel del mercurio. La temperatura del gas en grados Celsius será

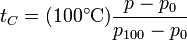
$t_C = (100^\circ\mathrm{C})\frac{p-p_0}{p_{100}-p_0}$

Lo que tiene de especial este termómetro es que permite obtener una escala absoluta. Supongamos que construimos cuatro termómetros de gas a volumen constante, cada uno con un gas diferente (hidrógeno, nitrógeno, oxígeno y neón, por ejemplo). Para una temperatura dada, por ejemplo la de fusión del azufre, cada uno de los termómetros dará una lectura ligeramente diferente. Pero si se va reduciendo la densidad del gas de la vasija, los valores medidos se van acercando y en el límite tienden al mismo valor, independientemente del gas concreto que se emplee. De esta forma podemos construir una escala de temperaturas absoluta como la que tendría un termómetro de gas a volumen constante en el límite en el que la densidad del gas se anula. Naturalmente, no se pueden anular del todo porque nos quedaríamos sin termómetro, pero se puede extrapolar y calcular cuánto mediría este termómetro ideal.

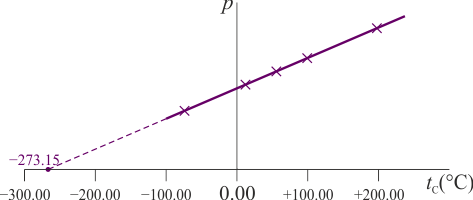
El resultado es que la presión del gas varía linealmente con la temperatura

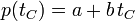
$p(t_C) = a + b\,t_C\,$

Podemos preguntarnos, para esta escala independiente del gas, a qué temperatura se anularía la presión del gas interior. El resultado es, experimentalmente

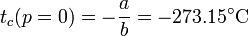
$t_c(p=0) = -\frac{a}{b}= -273.15^\circ\mathrm{C}$

para todos los gases empleados. Construimos entonces la temperatura absoluta

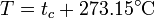
$T = t_c + 273.15^\circ\mathrm{C}$

y la presión del gas es simplemente proporcional a la temperatura absoluta

$p = b T\,$

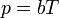
siendo b una constante que depende de la densidad del gas y otras constantes.

Equilibrio mecánico y térmico. Presión y temperatura (GIE)

De Laplace

Contenido

1 Presión

2 Sistemas en equilibrio mecánico

3 Principio cero de la termodinámica

3.1 Equilibrio térmico

3.2 Principio cero de la termodinámica

4 Medida de la temperatura

4.1 Termómetros

4.2 Escalas de temperatura

4.3 Temperatura absoluta

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES