Partícula moviéndose sobre una parábola, Noviembre 2014 (G.I.C.)
De Laplace
Contenido |
1 Enunciado
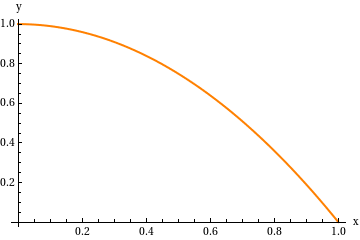
Una partícula se mueve siguiendo la trayectoria descrita por la curva de
ecuaciones implícitas y = A(1 − x2 / A2) y z = 0, donde A es una constante. La
coordenada x varía en el intervalo ![x\in[0,A]](/wiki/images/math/5/b/2/5b2bfc2aaf6f4df367b06d38ae81aa19.png) .
.
- Determina el vector tangente en función de la posición de la partícula
- Suponiendo que en t = 0 la distancia recorrida es s = 0 encuentra la expresión que da la distancia total recorrida sobre la curva.
- ¿Cuál es el vector normal a la trayectoria en x = 0?
2 Solución
2.1 Vector tangente
Podemos parametrizar la curva en función de la coordenada x
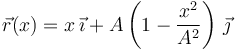
Calculamos el vector tangente usando la expresión
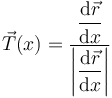
Derivando en la parametrización tenemos
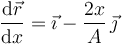
El módulo de este vector es
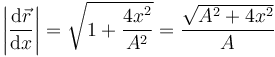
Por tanto el vector tangente es

2.2 Distancia recorrida
La distancia recorrida en un desplazamiento elemental es
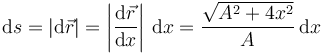
La distancia total recorrida es la suma de todos estos desplazamientos elementales, es decir
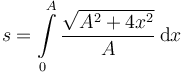
2.3 Vector normal en x = 0
La forma más fácil de encontrar este vector es dibujar la curva. A la derecha se muestra la gráfica escogiendo A = 1. Vemos que en x = 0 el vector normal es
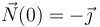
Otra forma más complicada es calcular el vector normal derivando el vector tangente,
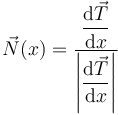
El resultado es

Evaluándolo en x = 0 obtenemos el resultado anterior.