Primera Convocatoria Ordinaria 2015/16 (MR G.I.C.)
De Laplace
Revisión a fecha de 20:05 29 ene 2016; Pedro (Discusión | contribuciones)
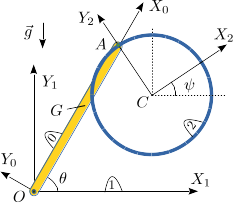
Aro colgando de una barra que rota
La barra homogénea OA (sólido "0") tiene masa m y longitud L. Está articulada en el punto fijo O y rota de modo que está siempre contenida en el plano OX1Y1. En su extremo A está articulado un aro homogéneo de radio R y masa m (sólido "2"). El sistema está sometido a la acción de la gravedad. Se recomienda utilizar los ángulos {θ,ψ} como coordenadas para resolver el problema.
- Determina las reducciones cinemáticas de los movimientos {01}, {21}, {20}.
- Calcula las energías cinética y potencial totales del sistema.
- Usando las herramientas de la Dinámica Analítica, encuentra las ecuaciones de movimiento.
- Se impone el vínculo cinemático
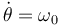. Determina el par necesario para imponer dicho vínculo. Supón que en el instante inicial se tiene θ(0) = 0, ψ(0) = 0.
- Supongamos que las coordenadas {θ,ψ} son de nuevo libres. Supón que se tiene θ(0) = 0, ψ(0) = 0. En ese instante una percusión
![\vec{\hat{F}}=[\hat{F}_0,\hat{F}_0,0]_1](/wiki/images/math/a/0/d/a0d931a1104a4fbfcf8b201fe4dc7018.png)
actúa sobre el punto A. Determina el estado cinemático del sistema justo después de la percusión.
