Preguntas de test de energía y leyes de conservación
De Laplace
Contenido |
1 Movimiento debido a una fuerza conservativa
Una partícula de masa 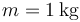 se mueve a lo largo del eje OX, sometida a la acción de una fuerza conservativa cuya energía potencial es la de la gráfica. Inicialmente se encuentra en
se mueve a lo largo del eje OX, sometida a la acción de una fuerza conservativa cuya energía potencial es la de la gráfica. Inicialmente se encuentra en 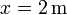 moviéndose hacia el semieje OX negativo con rapidez
moviéndose hacia el semieje OX negativo con rapidez  .
.

1.1 Pregunta 1
¿En qué punto se detiene por primera vez?
- A En
 .
.
- B En
 .
.
- C No se detiene nunca.
- D En
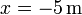 .
.
- A En
- Solución
La respuesta correcta es la D.
La partícula se encuentra inicialmente en 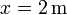 . De acuerdo con la gráfica, la energía potencial en este punto vale
. De acuerdo con la gráfica, la energía potencial en este punto vale

Además de esta energía potencial, la partícula posee una cierta energía cinética, de valor
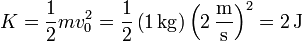
con lo que la energía mecánica de la partícula vale en el instante inicial
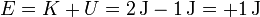
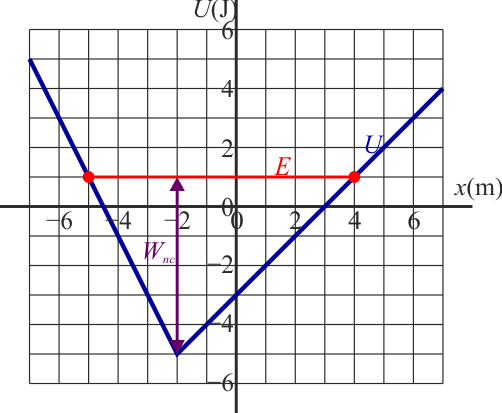
Puesto que la partícula se encuentra sometida solo a una fuerza conservativa, esta energía permanece constante, lo que se representa en la gráfica por una línea horiozntal

Esta gráfica nos describe completamente el movimiento. La partícula oscila entre los dos puntos de retorno, que son aquellos en que la línea de energía mecánica corta a la energía potencial. En ellos la energía cinética se hace cero, lo que quiere decir que en ellos la partícula se para. La detención es solo instantánea, pues al no ser nula la fuerza, la partícula comienza inmediatamente a moverse en sentido contrario.
Los dos puntos de retorno para esta energía están en 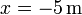 y
y 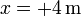 . Puesto que se nos dice que la partícula se mueve inicialmente en el sentido del eje OX negativo, el punto en el que se detiene (instantáneamente) por primera vez es
. Puesto que se nos dice que la partícula se mueve inicialmente en el sentido del eje OX negativo, el punto en el que se detiene (instantáneamente) por primera vez es
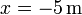
1.2 Pregunta 2
¿Qué tipo de movimiento describe la partícula entre  y un punto de retorno?
y un punto de retorno?
- A Uniformemente acelerado.
- B Sigue una ley complicada sin nombre específico.
- C Uniforme.
- D Armónico simple.
- Solución
La respuesta correcta es la A.
Debido a la conservación de la energía mecánica, la partícula se mueve de manera oscilatoria entre los dos puntos de retorno. Sin embargo, este movimiento no es armónico simple.
La fuerza que actúa sobre la partícula en cada punto la da la derivada de la energía respecto a la posición, cambiada de signo. Puesto que en la gráfica queda claro que la curva de potencial está formado por dos tramos rectilíneos, de pendiente constante, la fuerza en cada tramo entre el mínimo y un punto de retorno es constante.
El movimiento de una partícula sometida a una fuerza constante es uno de aceleración constante. Por tanto, el movimiento en cada tramo es uniformemente acelerado.
Podemos hallar la fuerza y la aceleración en cada tramo. La derivada en cada uno es igual a la pendiente de cada recta. Esta pendiente se puede calcular simplemente dividiendo un incremento en la vertical entre uno en la horizontal y resulta

Puesto que la masa es la unidad, los mismos valores nos dan la aceleración
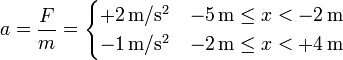
Conocida la aceleración podríamos determinar, si quisiéramos, como varía la posición con el tiempo o cuánto vale el periodo de oscilación.
1.3 Pregunta 3
Suponga que la masa se ve sometida adicionalmente a una fuerza de rozamiento que la va frenando hasta detenerla por completo. ¿Cuánta energía se disipa hasta que se detiene?
- A 5 J.
- B 6 J.
- C 1 J.
- D 2 J.
- Solución
La respuesta correcta es la B.
Si en el sistema existen fuerzas disipativas, la energía mecánica no se mantiene constante, sino que va decreciendo. Cuando la disipación consigue detener a la partícula por completo, el estado es el de energía cinética nula y mínima energía potencial. En este caso, esta situación se en  para la cual
para la cual 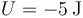 . Por tanto, la energía total disipada, en valor absoluto, es
. Por tanto, la energía total disipada, en valor absoluto, es

2 Fuerza que cambia de sentido
Una partícula de masa m que se mueve sobre el eje x se encuentra sometida a una fuerza conservativa que verifica la ley
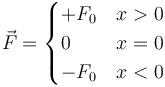
2.1 Pregunta 1
Tomando como origen de potencial x = 0, ¿cuál es la expresión de la energía potencial de la partícula?
- A
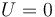
- B
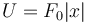
- C
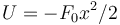
- D
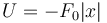
- A
- Solución
La respuesta correcta es la D.
La energía potencial en una dimensión viene definida por la integral

siendo x0 el origen de potencial, que en este caso es x0 = 0. Distinguimos dos casos, que sea x > 0 o que sea x < 0. En el primer caso
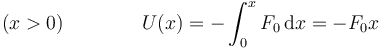
y en el segundo
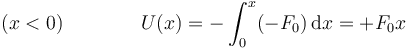
Reunimos los dos resultados
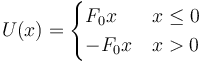
El valor U(x = 0) = 0 lo podemos colocar en cualquiera de las dos zonas por tratarse de una función continua.
Podemos escribir los dos tramos en una sola forma con ayuda de la función valor absoluto

lo que nos da

Gráficamente, la fuerza va como la función signo, mientras que la energía tiene una gráfica en forma de V invertida.
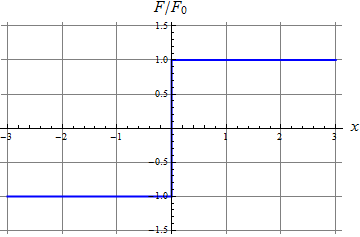
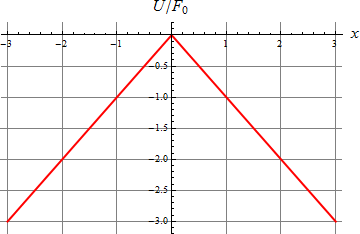
2.2 Pregunta 2
Para esta partícula la posición x = 0…
- A es de equilibrio indiferente.
- B es de equilibrio estable.
- C es de equilibrio inestable.
- D no es de equilibrio.
- Solución
La respuesta correcta es la C.
Un punto de equilibrio es inestable si al separar la partícula de la posición de equilibrio, la fuerza que actúa sobre ella tiende a separarla aun más. Esto es lo que ocurre en este caso. Si x > 0 la fuerza es positiva, es decir apunta hacia x creciente y por tanto aleja aun más a la partícula. A la inversa si x < 0.
Podemos verlo también empleando la gráfica de la energía, que tiene un máximo en x = 0, como corresponde a un punto de equilibrio inestable.
3 Otro caso de energía potencial
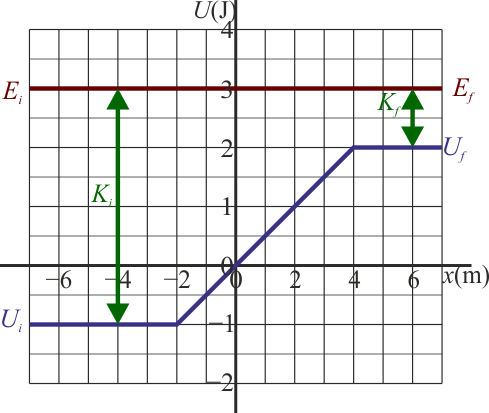
Una partícula de 2 kg se encuentra sometida a la energía potencial de la gráfica. Cuando se encuentra en  tiene una velocidad de +2 m/s. ¿Qué velocidad tiene cuando se encuentra en
tiene una velocidad de +2 m/s. ¿Qué velocidad tiene cuando se encuentra en 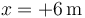 ?
?
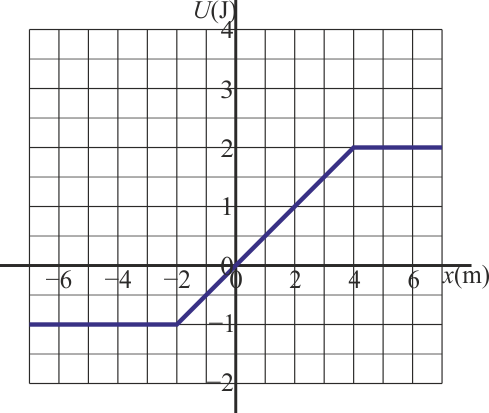
- A +1 m/s
- B − 1 m/s
- C Es imposible que llegue a
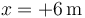 .
.
- D No hay información suficiente para responder la pregunta.
- Solución
La respuesta correcta es la A
La energía cinética inicial de la partícula es

lo que nos da una energía mecánica inicial
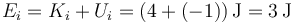
Esta energía se conserva, por lo que su valor cuando pasa por 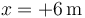 sigue siendo el mismo
sigue siendo el mismo
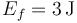
Esto nos permite conocer la energía cinética e ese punto

y de aquí obtenemos la rapidez final

Otra forma equivalente de llegar al resultado es observar que si todas las fuerzas son conservativas
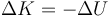
puesto que la energía potencial aumenta en 3J, la energía cinética debe disminuir en la misma cantidad.
4 Fuerza dependiente de la posición
Una partícula de masa 2 kg se mueve por el eje OX de forma que cuando pasa por x = 0 su velocidad es +3 m/s. Sobre la partícula actúa una fuerza en la dirección del mismo eje, 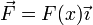 cuya gráfica es la de la
figura.
cuya gráfica es la de la
figura.
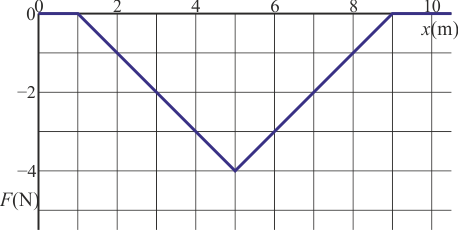
¿Cuál es la velocidad de la partícula cuando pasa por x = 10 m?
- A +5 m/s.
- B Es imposible que llegue a ese punto.
- C +3 m/s.
- D +11 m/s.
- Solución
La respuesta correcta es la B.
Aplicando el teorema de las fuerzas vivas tenemos que
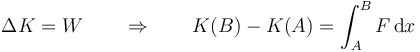
La energía cinética inicial vale
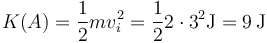
y el trabajo que se realiza sobre la partícula si recorre toda la distancia es el área entre la curva y el eje. Esta integral es negativa en este caso porque la fuerza lo es. Es decir, puesto que la fuerza es negativa se opone al movimiento de la partícula y reduce su energía cinética
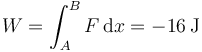
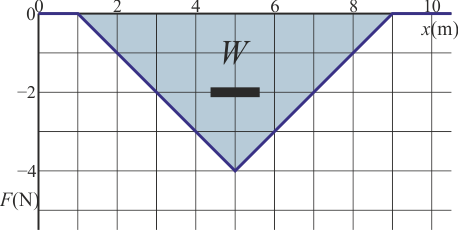
Por tanto, la energía cinética final sería

lo cual es imposible, ya que la energía cinética nunca puede ser negativa. Lo que ocurre realmente es que, al ser la fuerza opuesta al movimiento, llega un momento en que la detiene del todo y le da la vuelta. La partícula nunca llega a 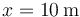 . El punto de retorno se dará en el momento en que el área entre la curva y el eje llegue a -9J.
. El punto de retorno se dará en el momento en que el área entre la curva y el eje llegue a -9J.

5 Fuerza dependiente de la posición (2ª versión)
Una partícula de masa 2 kg se mueve por el eje OX de forma que cuando pasa por x = 0 su velocidad es +3 m/s. Sobre la partícula actúa una fuerza en la dirección del mismo eje, 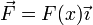 cuya gráfica es la de la figura.
cuya gráfica es la de la figura.

¿Cuál es la velocidad de la partícula cuando pasa por x = 10 m?
- A +5 m/s.
- B Es imposible que llegue a ese punto.
- C +3 m/s.
- D +11 m/s.
- Solución
La respuesta correcta es la A.
El teorema de las fuerzas vivas establece que
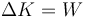
En este caso, empleando el SI para todas las variables
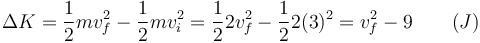
mientras que el trabajo es igual a la integral
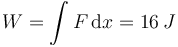
El valor de la integral corresponde al área bajo la curva, que en este caso es igual a la de un triángulo.
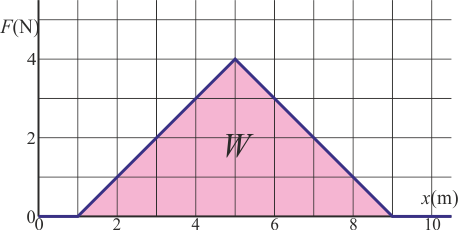
Este trabajo es positivo, como corresponde a que la fuerza vaya en el mismo sentido del movimiento y acelere la partícula.
Igualando las dos cantidades
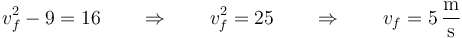
6 Comparación de movimiento de proyectiles
Tres proyectiles se lanzan desde lo alto de una torre de altura H y con la misma rapidez inicial v0. El proyectil “1” se lanza con un ángulo de elevación 30° respecto a la horizontal, el “2” en dirección puramente horizontal y el “3” con uno de 30° por debajo de la horizontal. ¿Cuál de los tres tendrá una mayor rapidez cuando impacte con el suelo, situado en z = 0? Despréciese el rozamiento con el aire.
- A El 3.
- B El 2.
- C Los tres la misma.
- D El 1.
- Solución
La respuesta correcta es la C.
Aplicando la ley de conservación de la energía mecánica tenemos que su valor inicial debe coincidir con el final. Para las tres partículas, en el instante inicial
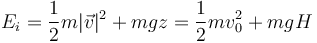
y en el final
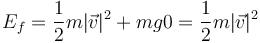
Por tanto, las tres masas llegan con la misma rapidez al suelo.

7 Movimiento por fuerza conservativa
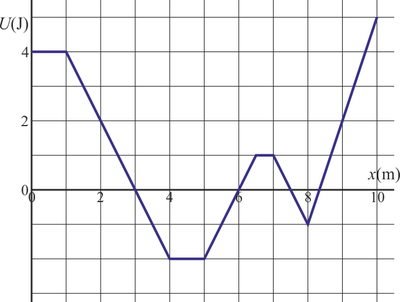
Una partícula de 1 kg se mueve sometida exclusivamente a una fuerza conservativa cuya energía potencial es la ilustrada en la figura:
7.1 Pregunta 1
Si la partícula parte de  con una rapidez de 2 m/s, ¿qué distancia recorre hasta que se para por primera vez?
con una rapidez de 2 m/s, ¿qué distancia recorre hasta que se para por primera vez?
- A 3 m
- B No hay información suficiente para saberlo.
- C 1 m
- D 6 m
- Solución
La respuesta correcta es la B.
No hay suficiente información porque no se dice si la partícula va hacia los x positivos o los negativos. Según el sentido del movimiento inicial, la distancia recorrida será diferente.
7.2 Pregunta 2
¿Cuánto vale la fuerza 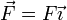 , ejercida sobre la partícula en su posición inicial?
, ejercida sobre la partícula en su posición inicial?
- A
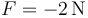
- B Es nula
- C
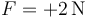
- D No hay información suficiente para saberlo.
- A
- Solución
La respuesta correcta es la C.
8 Coche en una curva
Un automóvil de 1200kg describe una semicircunferencia de 314 m de longitud con rapidez constante de 72km/h. Si lo tratamos como una partícula,…
8.1 Pregunta 1
¿cuánto vale en módulo la fuerza que actúa sobre él?
- A 62kN
- B 4.8kN
- C Es nula.
- D 150N
- Solución
La respuesta correcta es la B.
El vehículo describe un movimiento circular uniforme, con lo que su aceleración es puramente normal. De acuerdo con la segunda ley de Newton
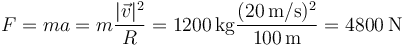
8.2 Pregunta 2
¿Qué trabajo realiza esta fuerza aplicada desde el principio al final de la semicircunferencia?
- A Es nulo.
- B 1.5MJ
- C 0.48MJ
- D -1.5MJ
- Solución
La respuesta correcta es la A.
La fuerza que actúa sobre la partícula es puramente normal, por lo que no realiza trabajo






