Fuerzas ficticias (GIE)
De Laplace
Contenido |
1 Introducción
Es común tanto en la vida diaria como en algunos libros de divulgación o de texto, el hablar de la “fuerza centrífuga'” como una fuerza real que mueve los objetos, empujándolos hacia afuera, responsable de que por ejemplo la Luna no se estrelle contra la Tierra. Incluso algún libro la identifica como la reacción a la fuerza centrípeta, que sería la acción.
Sin embargo, ¿quién ejerce la fuerza centrífuga? ¿Es eléctrica, gravitatoria o de qué tipo? ¿Si alguien ejerce una fuerza centrífuga sobre una partícula, ejercerá la partícula una fuerza centrífuga sobre ese alguien?
La respuesta es que nadie ejerce la fuerza centrífuga, porque la fuerza centrífuga no existe. Es una fuerza ficticia, un artificio matemático consecuencia de la generalización de las leyes de Newton a sistemas no inerciales.
Más adelante daremos la expresión matemática de esta fuerza ficticia, pero es fácil interpretarla con un ejemplo sencillo. Imaginemos un patinador montado en el interior de un vagón de tren, sin ningún tipo de rozamiento con el suelo.
Cuando el tren toma una curva hacia la izquierda, el patinador, sobre el que no actúa ninguna fuerza continúa en línea recta, con lo que finalmente es golpeado por la pared derecha del vagón. ¿Qué entiende el patinador (que solo ve el vagón y no el exterior)? Que de pronto ha actuado sobre él una fuerza hacia la derecha que ha terminado llevándolo hasta la pared. Pero esta fuerza es ficticia, es solo el resultado de emplear un sistema de referencia (el vagón) que está en rotación.
2 Sistema con aceleración lineal
Antes de analizar el caso de un sistema en rotación, consideraremos un caso más simple: el de un sistema de referencia que se traslada de forma acelerada respecto a uno inercial.
De nuevo, el ejemplo es el de un vagón de tren que se desplaza de manera acelerada por un camino ahora rectilíneo. Si del techo de este vagón cuelga un péndulo sabemos que el hilo se inclinará hacia atrás cuando el tren acelera y hacia adelante cuando frena. ¿Por qué lo hace? ¿Qué fuerza horizontal actúa sobre la masa para desviarlo de la vertical?
2.1 Interpretación por un observador inercial
Veamos cómo sería empleando las leyes de Newton en un sistema de referencia inercial, que sería el de un observador situado fuera del tren. Para este observador, la lenteja del péndulo se encuentra en reposo respecto al tren, es decir, se mueve aceleradamente respecto al observador. De acuerdo con la segunda ley de Newton esto implica que la masa no está en equilibrio, sino que debe haber una fuerza neta que actúa sobre ella. Las dos únicas fuerzas posibles son el peso y la tensión del hilo, por lo que
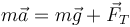
Separando en componentes
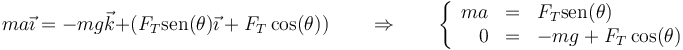
Si despejamos y dividimos nos queda, para el ángulo,
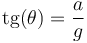
con lo cual, midiendo el ángulo, tenemos la aceleración, que podrá ser tanto positiva como negativa. Este es el principio de muchos acelerómetros.
Lo importante aquí es que (1) El péndulo no está en equilibrio, sino acelerado, (2) sobre la masa actúan dos fuerzas reales: peso y tensión y (3) la suma de las fuerzas no es cero.
Ahora bien, ¿cómo explica la inclinación un observador que va dentro del tren y por tanto no aprecia aceleración en la masa colgante?
2.2 Relación entre los sistemas de referencia
Para relacionar las medidas de los dos observadores debemos introducir dos sistemas de referencia:
- Uno inercial (usualmente llamado sistema laboratorio o sistema fijo) asociado al observador externo. Etiquetaremos este sistema como “1”. Su origen de coordenadas es el punto O_1 y sus vectores de la base canónica son {i ⃗_1,j ⃗_1,k ⃗_1 }.
- Uno no inercial (denominado sistema móvil), que sería el del tren. Etiquetaremos este sistema como “0”. Su origen de coordenadas es el punto O_0 y los vectores de su base canónica son {i ⃗_0,j ⃗_0,k ⃗_0 }.
- La partícula en sí misma constituye un cuerpo adicional que etiquetaremos como “2’’. Aunque en el contexto de cinemática de la partícula esta etiqueta es superflua (ya que la identificamos a la vez como P y como “2”), la mantendremos ya que sí es útil al estudiar el movimiento de un sólido y de esta manera se evitan confusiones.
Dado que el sistema móvil describe un movimiento rectilíneo sin rotación, los vectores de la base móvil son los mismos que los de la base fija. Más adelante veremos qué ocurre cuando hay rotación.
La posición de una partícula que se mueve respecto a los dos sistemas verifica la relación entre posiciones relativas (O_1 P) ⃗=(O_1 O_0 ) ⃗+(O_0 P) ⃗
Si derivamos aquí respecto al tiempo obtenemos una relación entre velocidades v ⃗_21^P=v ⃗_01+v ⃗_20^P siendo v ⃗_21^P y v ⃗_20^Plas velocidades de la partícula o respecto a los sistemas fijo y móvil, respectivamente y v ⃗_01 la velocidad instantánea con que se traslada el sistema móvil respecto al fijo.
Derivando de nuevo obtenemos una relación entre aceleraciones a ⃗_21^P=a ⃗_01+a ⃗_20^P





