Barra empujando placa deslizante (MR G.I.C.)
De Laplace
Contenido |
1 Enunciado
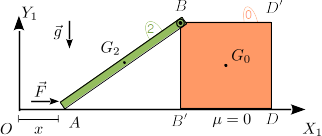
El sistema de sólidos de la figura está formado por una varilla (sólido "2", masa m, longitud 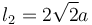 ) y por una placa cuadrada (sólido "0", masa m, lado l0 = 2a) articulados entre sí en el punto B. Sobre el eje OX1 se apoyan el extremo A de la barra y el lado BD del cuadrado. Todos los contactos son lisos. Sobre el extremo A se aplica una fuerza horizontal creciente
) y por una placa cuadrada (sólido "0", masa m, lado l0 = 2a) articulados entre sí en el punto B. Sobre el eje OX1 se apoyan el extremo A de la barra y el lado BD del cuadrado. Todos los contactos son lisos. Sobre el extremo A se aplica una fuerza horizontal creciente 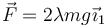 (λ = t / T), donde T es una constante. Inicialmente (t = 0), el sistema está en reposo y A coincide con O.
(λ = t / T), donde T es una constante. Inicialmente (t = 0), el sistema está en reposo y A coincide con O.
- Calcula la aceleración del sistema, los valores de las fuerzas vinculares y la posición de la fuerza normal en BD, todo ello en función del tiempo.
- Calcula el instante en que el vértice B' empieza a despegar (condición de vuelco) y el trabajo realizado hasta ese instante por la fuerza
 .
.
2 Solución
2.1 Cinemática del problema
Suponemos que el lado B'D de la placa no se levanta del suelo. Entonces los dos sólidos realizan una traslación. Las reducciones cinemáticas de los tres movimientos son las siguintes.
Movimiento {21}
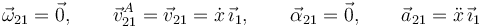
Movimiento {01}
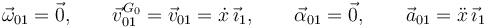
Movimiento {20}
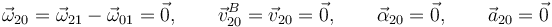
Al ser traslaciones, las velocidades son las mismas en todos los puntos del sólido. Por eso no es necesario poner las letras en los vectores velocidad.
2.2 Fuerzas que actúan sobre cada sólido
La figura de la derecha muestra las fuerzas que actúan sobre los sólidos "0" y "2", asi como las dimensiones de la placa, la barra y la distancia entre los puntos A y B'. Expresamos estas fuerzas en el sistema de ejes de la figura Para el sólido "0 tenemos
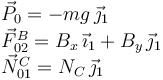
Y para el sólido "2"
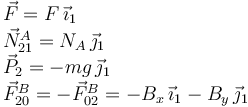
Hemos utilizado que, por la Tercera Ley de Newton, 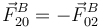 . Al ser todos los vínculos lisos las fuerzas en los contactos A y C son perpendiculares a las superficies.
. Al ser todos los vínculos lisos las fuerzas en los contactos A y C son perpendiculares a las superficies.
Tenemos 6 incógnitas, a saber
{x,Bx,By,NC,NA,δ}
Tendremos 6 ecuaciones, provenientes de aplicar el T.C.M. y el T.M.C. a los dos sólidos. Aplicamos el T.C.M. a los dos sólidos
T.C.M. para el sólido "2":
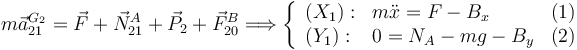
T.C.M. para el sólido "0":
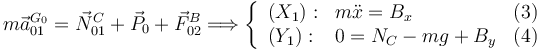
Ahora aplicamos el T.M.C. en el centro de masas de cada sólido.
T.M.C. para el sólido "2":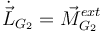
Calculamos los momentos sobre el sólido "2"
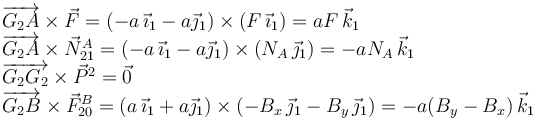
Por tanto el momento total de las fuerzas externas es
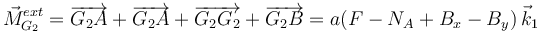
Por otro lado, el momento cinético respecto a G2 es
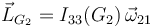
y su derivada temporal es
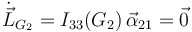
Aplicando el T.M.C. obtenemos la ecuación
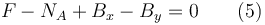
Hacemos lo mismo para el sólido "0". El T.M.C. nos dice 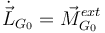 Calculamos los momentos
Calculamos los momentos
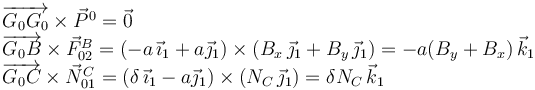
Por tanto el momento total de las fuerzas externas es

Por otro lado, el momento cinético respecto a G0 es
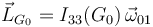
y su derivada temporal es
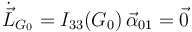
Aplicando el T.M.C. obtenemos la ecuación