Ejemplos de velocidad en función de la posición

De Laplace

Revisión a fecha de 19:22 28 oct 2015; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Primer caso
3 Segundo caso

1 Enunciado

1) La velocidad de una partícula sigue la ley

$v = \sqrt{Ax}$

siendo $x$ la distancia recorrida desde el instante inicial.

Calcule la aceleración de la partícula. ¿Qué tipo de movimiento describe?

2) Una partícula se mueve en línea recta, cumpliendo su velocidad instantánea

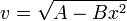
$v = \sqrt{A- B x^2}$

con $A$ y $B$ constantes positivas.

¿En que se medirá $B$ en el SI?
¿Cómo depende de la posición la aceleración de la partícula?

2 Primer caso

La aceleración la obtenemos derivando la velocidad respecto al tiempo, lo cual se consigue aplicando la regla de la cadena,

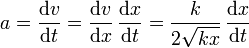
$a = \frac{\mathrm{d}v}{\mathrm{d}t}=\frac{\mathrm{d}v}{\mathrm{d}x}\,\frac{\mathrm{d}x}{\mathrm{d}t}=\frac{k}{2\sqrt{kx}}\,\frac{\mathrm{d}x}{\mathrm{d}t}$

pero la derivada de la posición respecto al tiempo es la propia velocidad, por lo que

$a = \frac{k}{2\sqrt{kx}}\,v = \frac{k}{2\sqrt{kx}}\sqrt{kx} = \frac{k}{2}$

La aceleración es por tanto constante y el movimiento es uniformemente acelerado.

También puede calcularse directamente a partir de la relación

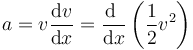
$a = v\frac{\mathrm{d}v}{\mathrm{d}x}=\frac{\mathrm{d}\ }{\mathrm{d}x}\left(\frac{1}{2}v^2\right)$

que en este caso da

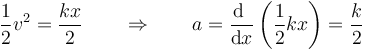
$\frac{1}{2}v^2= \frac{kx}{2} \qquad\Rightarrow\qquad a = \frac{\mathrm{d}\ }{\mathrm{d}x}\left(\frac{1}{2}kx\right)=\frac{k}{2}$

3 Segundo caso

Para el segundo caso operamos de forma análoga

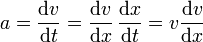
$a = \frac{\mathrm{d}v}{\mathrm{d}t}=\frac{\mathrm{d}v}{\mathrm{d}x}\,\frac{\mathrm{d}x}{\mathrm{d}t}= v\frac{\mathrm{d}v}{\mathrm{d}x}$

La velocidad puede meterse dentro de la derivada observando que

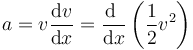
$a = v\frac{\mathrm{d}v}{\mathrm{d}x} = \frac{\mathrm{d}\ }{\mathrm{d}x}\left(\frac{1}{2}v^2\right)$

En este caso

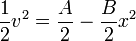
$\frac{1}{2}v^2 = \frac{A}{2}-\frac{B}{2}x^2$

con lo que la aceleración vale

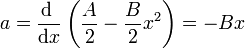
$a = \frac{\mathrm{d}\ }{\mathrm{d}x}\left(\frac{A}{2}-\frac{B}{2}x^2\right) = - Bx$

Vemos que la aceleración es proporcional a la posición cambiada de signo, por lo que esta velocidad corresponde a un movimiento armónico simple.

En cuanto las dimensiones de $B$ tenemos que la raíz cuadrada del producto por $x 2$ debe dar una velocidad, por lo que

$\frac{L}{T} = \left([B]L^2\right)^{1/2}\qquad \Rightarrow\qquad [B] = T^{-2}$

y por tanto se mide en $s - 2$ en el SI. De la relación entre la aceleración y la posición vemos que $B = ω 2$ lo que es coherente con estas unidades.

Ejemplos de velocidad en función de la posición

De Laplace

Contenido

1 Enunciado

2 Primer caso

3 Segundo caso

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES