4.1. Estudio de la velocidad de tres puntos

De Laplace

Revisión a fecha de 09:36 24 sep 2015; Pedro (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Condición de rigidez
3 Velocidad del origen
4 Velocidad del punto P
5 Puntos con velocidad instantánea nula
- 5.1 A partir de la ecuación del campo de velocidades
- 5.2 Cálculo del eje central

1 Enunciado

En un hipotético sólido rígido, las posiciones y velocidades de tres puntos son respectivamente:

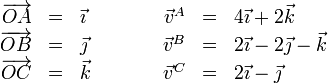
$\begin{array}{rclcrcl} \overrightarrow{OA}&=&\vec{\imath}&\qquad & \vec{v}^A & = & 4\vec{\imath}+2\vec{k}\\ \overrightarrow{OB}&=&\vec{\jmath}&\qquad & \vec{v}^B& = &2\vec{\imath}-2\vec{\jmath}-\vec{k}\\ \overrightarrow{OC}&=&\vec{k}&\qquad & \vec{v}^C&=&2\vec{\imath}-\vec{\jmath} \end{array}$

Demuestre que estas velocidades son compatibles con la condición de rigidez.
Halle la velocidad del punto $O (0,0,0)$ .
Calcule la velocidad del punto $\overrightarrow{OP}=2\vec{\imath}-2\vec{\jmath}-\vec{k}$ .
¿Existe algún punto que tenga velocidad nula? ¿Dónde estaría situado?

Todas las cantidades están expresadas en las unidades del SI.

2 Condición de rigidez

Para que un movimiento sea posible en un sólido rígido debe cumplirse, para todos y cada uno de sus pares de puntos la condición cinemática de rigidez, consistente en la equiproyectividad del campo de velocidades:

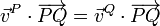
$\vec{v}^P\cdot\overrightarrow{PQ}=\vec{v}^Q\cdot\overrightarrow{PQ}$

Aplicando esta condición para cada par de partículas resulta:

Partículas A y B

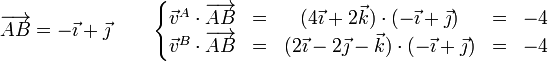
$\overrightarrow{AB}=-\vec{\imath}+\vec{\jmath}\qquad\left\{\begin{matrix}\vec{v}^A\cdot\overrightarrow{AB} & = & (4\vec{\imath}+2\vec{k})\cdot(-\vec{\imath}+\vec{\jmath}) & = & -4 \\ \vec{v}^B\cdot\overrightarrow{AB} & = & (2\vec{\imath}-2\vec{\jmath}-\vec{k})\cdot(-\vec{\imath}+\vec{\jmath}) & = & -4 \end{matrix}\right.$

Partículas A y C

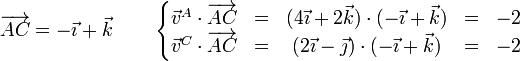
$\overrightarrow{AC}=-\vec{\imath}+\vec{k}\qquad\left\{\begin{matrix}\vec{v}^A\cdot\overrightarrow{AC} & = & (4\vec{\imath}+2\vec{k})\cdot(-\vec{\imath}+\vec{k}) & = & -2 \\ \vec{v}^C\cdot\overrightarrow{AC} & = & (2\vec{\imath}-\vec{\jmath})\cdot(-\vec{\imath}+\vec{k}) & = & -2 \end{matrix}\right.$

Partículas B y C

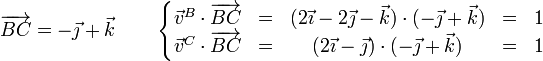
$\overrightarrow{BC}=-\vec{\jmath}+\vec{k}\qquad\left\{\begin{matrix}\vec{v}^B\cdot\overrightarrow{BC} & = & (2\vec{\imath}-2\vec{\jmath}-\vec{k})\cdot(-\vec{\jmath}+\vec{k}) & = & 1 \\ \vec{v}^C\cdot\overrightarrow{BC} & = & (2\vec{\imath}-\vec{\jmath})\cdot(-\vec{\jmath}+\vec{k}) & = & 1 \end{matrix}\right.$

Puesto que los tres pares verifican la condición, estas velocidades son compatibles con un movimiento de un sólido rígido.

3 Velocidad del origen

La velocidad de cualquier otro punto se puede obtener aplicando la equiproyectividad con los tres puntos que ya tenemos. Si la velocidad de O es

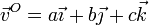
$\vec{v}^O = a\vec{\imath}+b\vec{\jmath}+c\vec{k}$

la condición cinemática de rigidez nos da, para el par formado por O y A

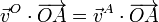
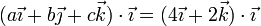
$\vec{v}^O\cdot\overrightarrow{OA}= \vec{v}^A\cdot\overrightarrow{OA}$ $\Rightarrow$ $(a\vec{\imath}+b\vec{\jmath}+c\vec{k})\cdot\vec{\imath}=(4\vec{\imath}+2\vec{k})\cdot\vec{\imath}$ $\Rightarrow$ $a=4\,$

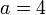
Para O y B

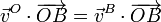
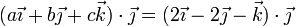
$\vec{v}^O\cdot\overrightarrow{OB}=\vec{v}^B\cdot\overrightarrow{OB}$ $\Rightarrow$ $(a\vec{\imath}+b\vec{\jmath}+c\vec{k})\cdot\vec{\jmath}= (2\vec{\imath}-2\vec{\jmath}-\vec{k})\cdot\vec{\jmath}$ $\Rightarrow$ $b=-2\,$

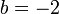
Y para O y C

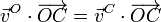
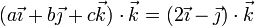
$\vec{v}^O\cdot\overrightarrow{OC}=\vec{v}^C\cdot\overrightarrow{OC}$ $\Rightarrow$ $(a\vec{\imath}+b\vec{\jmath}+c\vec{k})\cdot\vec{k}= (2\vec{\imath}-\vec{\jmath})\cdot\vec{k}$ $\Rightarrow$ $c=0\,$

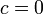
Reuniendo los tres resultados obtenemos la velocidad

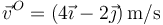
$\vec{v}^O = (4\vec{\imath}-2\vec{\jmath})\,\mathrm{m/s}$

4 Velocidad del punto P

El mismo procedimiento puede emplearse para cualquier otro punto, si bien en general resultará un sistema de ecuaciones lineales. Si la velocidad del punto P es de la forma

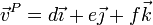
$\vec{v}^P = d\vec{\imath}+e\vec{\jmath}+f\vec{k}$

resultan las ecuaciones

Para P y A

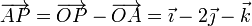
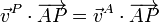
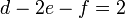
$\overrightarrow{AP}=\overrightarrow{OP}-\overrightarrow{OA}=\vec{\imath}-2\vec{\jmath}-\vec{k}$ $\vec{v}^P\cdot\overrightarrow{AP}= \vec{v}^A\cdot\overrightarrow{AP}$ $\Rightarrow$ $d-2e-f=2\,$

Para P y B

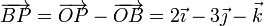
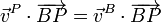
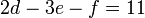
$\overrightarrow{BP}=\overrightarrow{OP}-\overrightarrow{OB}=2\vec{\imath}-3\vec{\jmath}-\vec{k}$ $\vec{v}^P\cdot\overrightarrow{BP}= \vec{v}^B\cdot\overrightarrow{BP}$ $\Rightarrow$ $2d-3e-f=11\,$

Para P y C

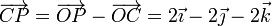
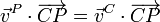
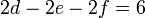
$\overrightarrow{CP}=\overrightarrow{OP}-\overrightarrow{OC}=2\vec{\imath}-2\vec{\jmath}-2\vec{k}$ $\vec{v}^P\cdot\overrightarrow{CP}= \vec{v}^C\cdot\overrightarrow{CP}$ $\Rightarrow$ $2d-2e-2f=6\,$

Tenemos entonces el sistema de ecuaciones

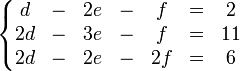
$\left\{\begin{matrix}d & - & 2e & - & f & = & 2 \\ 2d& - & 3e & - & f & = & 11 \\ 2d & - &2e & -& 2f &= & 6\end{matrix}\right.$

con solución

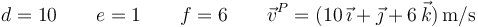
$d = 10\qquad e = 1\qquad f = 6\qquad\vec{v}^P = (10\,\vec{\imath}+\vec{\jmath}+6\,\vec{k})\,\mathrm{m/s}$

Un procedimiento alternativo para calcular la velocidad de un cuarto punto del sólido rígido, conocidas las velocidades de tres puntos no alineados, consiste en determinar primero el vector velocidad angular 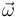$\vec{\omega}\,$ . Las velocidades conocidas están obligadas a satisfacer la ecuación del campo de velocidades. Así, por ejemplo:

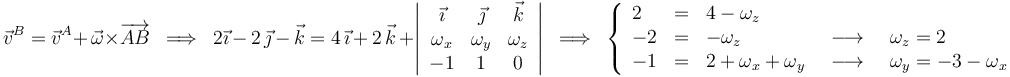
$\vec{v}^{B}=\vec{v}^{A}+\,\vec{\omega}\times\overrightarrow{AB}\,\,\,\Longrightarrow\,\,\,2\vec{\imath}\, -\, 2\,\vec{\jmath}\, -\,\vec{k}=4\,\vec{\imath}\, +\,2\,\vec{k}\,+\left|\begin{array}{ccc} \vec{\imath} & \vec{\jmath} & \vec{k} \\ \omega_x & \omega_y & \omega_z \\ -1 & 1 & 0 \end{array}\right|\,\,\,\Longrightarrow\,\,\,\left\{\begin{array}{lllll} 2 & = & 4-\omega_z & & \\ -2 & = & -\omega_z &\,\,\,\longrightarrow\,\,\,& \omega_z=2 \\ -1 & = & 2+\omega_x+\omega_y & \,\,\,\longrightarrow\,\,\, & \omega_y=-3-\omega_x \end{array} \right.$

Y por otra parte:

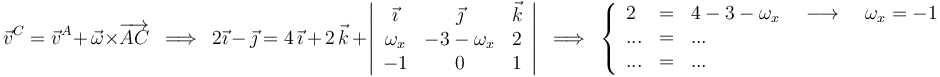
$\vec{v}^{C}=\vec{v}^{A}+\,\vec{\omega}\times\overrightarrow{AC}\,\,\,\Longrightarrow\,\,\,2\vec{\imath}\, -\, \vec{\jmath}=4\,\vec{\imath}\, +\,2\,\vec{k}\,+\left|\begin{array}{ccc} \vec{\imath} & \vec{\jmath} & \vec{k} \\ \omega_x & -3-\omega_x & 2 \\ -1 & 0 & 1 \end{array}\right|\,\,\,\Longrightarrow\,\,\,\left\{\begin{array}{lllll} 2 & = & 4-3-\omega_x & \,\,\,\longrightarrow\,\,\, & \omega_x=-1 \\ ... & = & ... & & \\ ... & = & ... & & \end{array} \right.$

Ya tenemos información suficiente para escribir el vector velocidad angular:

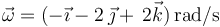
$\vec{\omega}=(-\vec{\imath}-2\,\vec{\jmath}+\,2\vec{k})\,\mathrm{rad/s}$

Y ahora, una vez conocido 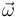$\vec{\omega}\,$ , se puede calcular la velocidad de cualquier punto utilizando de nuevo la ecuación del campo de velocidades:

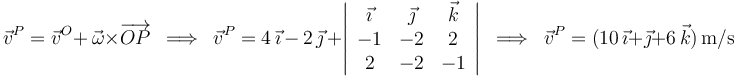
$\vec{v}^{P}=\vec{v}^{O}+\,\vec{\omega}\times\overrightarrow{OP}\,\,\,\Longrightarrow\,\,\,\vec{v}^{P}=4\,\vec{\imath}\, -\,2\,\vec{\jmath}\,+\left|\begin{array}{ccc} \vec{\imath} & \vec{\jmath} & \vec{k} \\ -1 & -2 & 2 \\ 2 & -2 & -1 \end{array}\right|\,\,\,\Longrightarrow\,\,\,\vec{v}^{P}=(10\,\vec{\imath}+\vec{\jmath}+6\,\vec{k})\,\mathrm{m/s}$

5 Puntos con velocidad instantánea nula

5.1 A partir de la ecuación del campo de velocidades

Se trata de buscar un punto (o un conjunto de ellos), I, tales que:

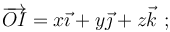
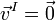
$\overrightarrow{OI}=x\vec{\imath}+y\vec{\jmath}+z\vec{k}\,\,;$ $\vec{v}^I = \vec{0}$

Apoyándonos en la velocidad ya conocida del punto $O\,$ , podemos escribir:

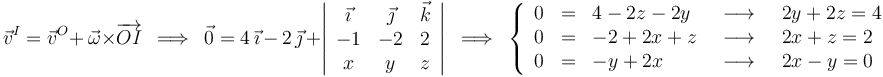
$\vec{v}^I=\vec{v}^O+\,\vec{\omega}\times\overrightarrow{OI}\,\,\,\Longrightarrow\,\,\,\vec{0}=4\,\vec{\imath}\, -\,2\,\vec{\jmath}\,+\left|\begin{array}{ccc} \vec{\imath} & \vec{\jmath} & \vec{k} \\ -1 & -2 & 2 \\ x & y & z \end{array}\right|\,\,\,\Longrightarrow\,\,\,\left\{\begin{array}{lllll} 0 & = & 4-2z-2y & \,\,\,\longrightarrow\,\,\, & 2y+2z=4 \\ 0 & = & -2+2x+z &\,\,\,\longrightarrow\,\,\,& 2x+z=2 \\ 0 & = & -y+2x & \,\,\,\longrightarrow\,\,\, & 2x-y=0 \end{array} \right.$

Por tanto, el sistema de ecuaciones cuya solución nos da la posición de los puntos de velocidad instantánea nula es:

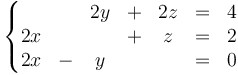
$\left\{\begin{matrix} & & 2y & + & 2z & = & 4 \\ 2x& & & + & z & = & 2 \\ 2x & - &y & & &= & 0\end{matrix}\right.$

Este sistema es compatible indeterminado. Podemos prescindir de la primera ecuación porque es linealmente dependiente de las otras dos (se obtiene restándole la tercera ecuación multiplicada por 2 a la segunda ecuación multiplicada por 2). Podemos quedarnos, pues, con el sistema de dos ecuaciones:

$\left\{\begin{matrix} 2x+z & = & 2 & \,\,\,\longrightarrow\,\,\, & z & = & 2-2x\\ 2x-y & = & 0 & \,\,\,\longrightarrow\,\,\, & y & = & 2x \end{matrix}\right.$

Por tanto, obtenemos un conjunto infinito de soluciones, situadas sobre la recta

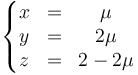
$\left\{\begin{matrix}x & = & \mu \\ y & = & 2\mu \\ z & = & 2-2\mu\end{matrix}\right.$ $\Rightarrow$ $\overrightarrow{OI}=[2\vec{k}+\mu(\vec{\imath}+2\vec{\jmath}-2\vec{k})]\,\mathrm{m}$

5.2 Cálculo del eje central

Otra forma más directa de llegar a la solución consiste en caer en la cuenta de que, si existen puntos de velocidad instantánea nula, seguro que esos puntos pertenecen al eje central del campo de velocidades (lugar geométrico de los puntos cuya velocidad tiene módulo mínimo). Por tanto, lo primero que hacemos es confirmar que efectivamente, en el ejercicio que nos ocupa, la velocidad en los puntos del eje central es nula:

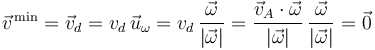
$\vec{v}^{\,\mathrm{min}}=\vec{v}_d=v_d\,\vec{u}_{\omega}=v_d\,\frac{\vec{\omega}}{|\vec{\omega}|}=\frac{\vec{v}_A\cdot\vec{\omega}}{|\vec{\omega}|}\,\frac{\vec{\omega}}{|\vec{\omega}|}=\vec{0}$

Y localizamos dichos puntos mediante la ecuación vectorial del eje central:

$\overrightarrow{OI}=\frac{\vec{\omega}\times\vec{v}^{\, O}}{|\vec{\omega}|^2}+\lambda\,\vec{\omega}=\left[\frac{4}{9}\,\vec{\imath}+\frac{8}{9}\,\vec{\jmath}+\frac{10}{9}\,\vec{k}+\lambda\,(-\vec{\imath}-2\,\vec{\jmath}+2\,\vec{k})\right]\,\mathrm{m}$

Esta ecuación parece diferente de la obtenida por el procedimiento anterior, pero en realidad ambas corresponden a la misma recta. En efecto, si hacemos el cambio de parámetro:

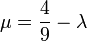
$\mu = \frac{4}{9}-\lambda$

podemos comprobar cómo la anterior ecuación se convierte en ésta de ahora.

4.1. Estudio de la velocidad de tres puntos

De Laplace

Contenido

1 Enunciado

2 Condición de rigidez

3 Velocidad del origen

4 Velocidad del punto P

5 Puntos con velocidad instantánea nula

5.1 A partir de la ecuación del campo de velocidades

5.2 Cálculo del eje central

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES