Mezcla de agua y vapor de agua
De Laplace
1 Enunciado
Se tiene un recipiente cilíndrico de paredes adiabáticas y con pistón móvil también adiabático, inmerso en un ambiente a 300 K y 101.3 kPa de presión. Dentro del recipiente se ponen en contacto 1 kg de agua a 100 °C (“subsistema 1”) con 1 m³ de vapor de agua a 200 ° (“subsistema 2”).
El agua puede considerarse un líquido incompresible de densidad 958.4 kg/m³.
El vapor de agua puede suponerse un gas ideal tal que a 100 °C y 101.3 kPa tiene una densidad de masa de 0.598 kg/m\tss{3}. En todo el rango 100 °C − 200 °C su calor específico promedio vale  .
.
La entalpía específica de vaporización a 100 °C y 101.3 kPa vale 2257 kJ/kg.
- Calcule, para una vez que se ha alcanzado el equilibrio térmico, qué cantidad de agua y de vapor de agua tenemos en el sistema. ¿Cuál es la proporción de la masa de vapor de agua respecto a la masa total?
- Calcule la variación de energía interna y de entalpía del sistema completo y de cada subsistema en este proceso, así como el trabajo realizado sobre el sistema completo y sobre cada subsistema.
2 Estado final
Puesto que el sistema completo está aislado térmicamente, toda la transferencia de calor será interna. Habrá una cierta cantidad de calor que pase del vapor de agua (que está más caliente) al agua saturada (que está más fría).
Por ser el pistón móvil, la presión del sistema permanece constante en todo momento, ya que el cambio de volumen hace subir o bajar el pistón, pero siempre en equilibrio mecánico con la presión exterior.
En el estado final, el vapor de agua habrá bajado a 100°C, mientras que parte del agua se habrá evaporado (puesto que ya está saturada no se calienta más, sino que todo el calor que le llega la hace pasar a la fase gaseosa).
Puesto que la evaporación del agua requiere mucha energía, no se va a evaporar toda el agua líquida.
El primer paso es conocer cuanta masa de agua en forma de vapor tenemos inicialmente, ya que la cantidad máxima de calor que podemos extraer de ella es
Para hallar la masa tenemos la densidad y el volumen, pero a distintas temperaturas, por lo que debemos calcular el volumen que ocupa el vapor de agua a 100°C. Por ser un gas ideal a presión constante se cumple la ley de Charles
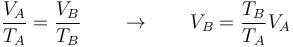
Sustituimos los valores numéricos

Por tanto, al enfriarse, el vapor del agua reduce su volumen. Ahora sí podemos calcular la masa de vapor que forma el subsistema 2&rdquo
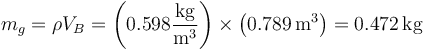
Una vez que tenemos la masa, podemos hallar la cantidad de calor que extraemos del subsistema 2 al bajar su temperatura 100 °C (o 100 K)
Vemos que la cantidad de calor es pequeña comparada con la entalpía de vaporización del agua.
La cantidad de agua líquida que pasamos a la fase gaseosa la sacamos de
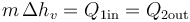
lo que nos da
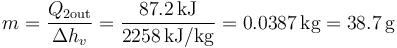
Por tanto, en el estado final nos queda una cantidad de agua líquida
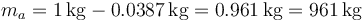
mientras que la masa total de agua en forma de vapor es

la temperatura de ambas fases es de 100°C pues están en equilibrio térmico.
La proporción de vapor de agua respecto a la masa total es