Preguntas de test de electrostática en el vacío (GIE)
De Laplace
1 Flujo de cuatro cargas en un cuadrado
Se tienen cuatro cargas en los vértices consecutivos de un cuadrado ABCD de lado  , siendo sus valores
, siendo sus valores 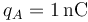 ,
, 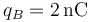 ,
, 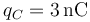 ,
, 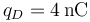 . ¿Cuánto vale el flujo del campo eléctrico multiplicado por
. ¿Cuánto vale el flujo del campo eléctrico multiplicado por  a través de una esfera centrada en la primera carga y de radio 12 cm?
a través de una esfera centrada en la primera carga y de radio 12 cm?
- A 6 nC
- B 1 nC
- C 10 nC
- D 7 nC
- Solución
La respuesta correcta es la D.
El lado del cuadrado mide 10 cm y su diagonal algo más de 14 cm. Por tanto, una esfera de 12 incluye a la propia carga qA y a sus dos vecinas qB y qD, pero no a la diagonalmente opuesta. Por tanto
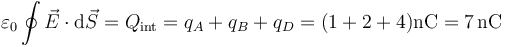
2 Fuerza de cuatro cargas en un cuadrado
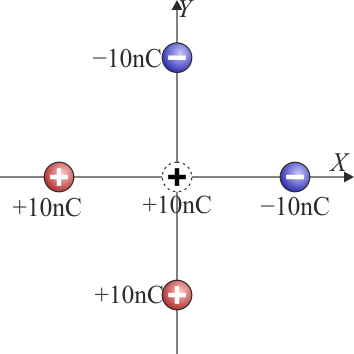
Se tienen cuatro cargas en los vértices de un cuadrado cuya diagonal mide 20 cm, según ilustra la figura. Los valores de todas las cargas son +10 nC o − 10 nC
2.1 Pregunta 1
¿Cuánto vale aproximadamente la fuerza sobre una carga de 10 nC situada en el centro del cuadrado?
- A
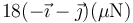
- B
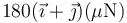
- C Es nula
- D
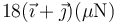
- A
- Solución
La respuesta correcta es la B.
El par de cargas situadas sobre el eje Z produce una fuerza neta en el sentido del eje X positivo. Las dos cargas sobre el eje Y una fuerza igual en el sentido del eje Y. La fuerza total tendrá entonces iguales componentes en los dos ejes e irá en el sentido del primer cuadrante. Esto reduce las posibles respuestas a la B o a la D. Para saber cuál es la correcta debemos aplicar la ley de Coulomb.
La fuerza debida a la carga situada en la parte negativa del eje X es
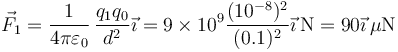
La debida a la carga situada en la parte positiva del eje X es igual a esta. Las de las cargas en el eje Y iguales pero en el sentido de 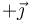 . Por tanto, la fuerza neta es
. Por tanto, la fuerza neta es
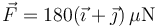
2.2 Pregunta 2
¿Cuánto vale aproximadamente el trabajo para llevar la carga central hasta el infinito?
- A No hay información suficiente para hallarlo.
- B −36 μJ.
- C +36 μJ.
- D Es nulo.
- Solución
La respuesta correcta es la D.
El punto central se encuentra en una posición simétrica respecto a las dos cargas de la misma magnitud y signo opuesto situadas en el eje Z. Lo mismo ocurre con las del eje Y. Por tanto, el potencial al que se encuentra la carga es nulo
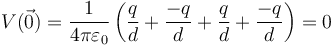
Dado que el infinito también se encuentra a potencial nulo, el trabajo para ir de un punto a otro es cero.
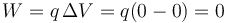
2.3 Pregunta 3
Suponiendo que no está la carga central, ¿cuánto vale la energía electrostática almacenada en el sistema?
- A Es nula.
- B −9 μJ.
- C +9 μJ.
- D No hay información suficiente para hallarla.
- Solución
La respuesta correcta es la B.
Cada carga se encuentra sometido al potencial de dos cargas opuestas situadas simétricamente (cuyos potenciales respectivos se anulan) y de una de signo opuesto, que produce una energía potencial negativa.
Por tanto, la energía electrostática total es la suma de cuatro términos negativos y la única respuesta posible es la B.
Podemos hallar el valor de la energía.
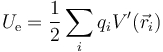
siendo 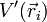 el potencial en cada carga debido al resto de cargas del sistema. Para la carga del eje X negativo vale
el potencial en cada carga debido al resto de cargas del sistema. Para la carga del eje X negativo vale
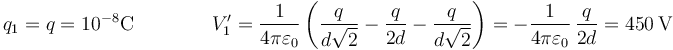
Lo que da una contribución para esta carga
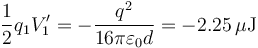
Operando igualmente para las otras tres cargas obtenemos
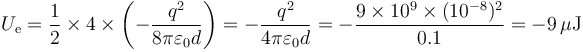
3 Distribución de carga en esfera
Se tiene únicamente una distribución uniforme de una carga Q < 0 sobre una superficie esférica de radio a. Para los tres puntos de la figura,
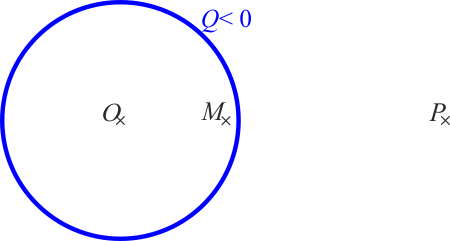
3.1 Pregunta 1
¿En cuál es mayor en módulo el campo eléctrico?
- A En M.
- B En O.
- C No hay información suficiente para saberlo.
- D En P.
- Solución
La respuesta correcta es la D.
En los puntos O y M es nulo el campo eléctrico. En P no, por tanto, en este punto es mayor, en módulo, el campo eléctrico.
3.2 Pregunta 2
¿Cómo se ordena el potencial de los tres puntos?
- A
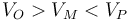 .
.
- B
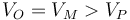 .
.
- C
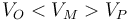 .
.
- D
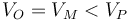 .
.
- A
- Solución
La respuesta correcta es la D.
Por ser nulo el campo eléctrico en el interior de la esfera, los puntos O y M se hallan al mismo potencial.
Al ser negativa la carga de la esfera, el campo eléctrico apunta hacia la esfera, es decir, de P a M (y O). Puesto que el campo va de más a menos potencial, esto quiere decir que P se encuentra a un potencial más alto que los otros dos puntos.
4 Energía de dos cargas
Dos cargas puntuales positivas q1 y q2 se encuentran a una distancia a. Si la distancia entre ellas se reduce a la mitad, ¿cómo cambia la energía electrostática del sistema?
- A Aumenta al cuádruple
- B Se reduce a la mitad.
- C Aumenta al doble.
- D No cambia.
- Solución
La respuesta correcta es la C.
La energía electrostática de un sistema de dos cargas es igual a
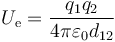
es decir, es inversamente proporcional a la distancia entre las cargas. Si esta se reduce a la mitad, la energía aumenta al doble.
5 Cargas en una barra
En los dos extremos de una barra rígida se encuentran cargas de la misma magnitud y signo opuesto. La barra se encuentra inicialmente en reposo y sumergida en un campo eléctrico uniforme, formando un cierto ángulo con el campo. ¿Qué efecto produce el campo sobre la barra?
- A Ninguno. Las fuerzas se cancelan y la barra permanece en reposo.
- B Produce un par de fuerzas que tiende a alinear la barra con el campo.
- C Produce un par de fuerzas que tiende a colocar la barra perpendicular al campo.
- D Produce una fuerza neta que tiende a desplazar la barra.
- Solución
La respuesta correcta es la B.
La fuerza sobre cada carga es igual al producto de ésta por el campo externo
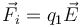
Al ser las cargas iguales en magnitud y de signo opuesto, y el campo uniforme, la resultante de las fuerzas es nula
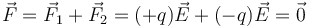
Sin ambargo, el momento de las fuerzas no se anula. Si las cargas están en los puntos A y B
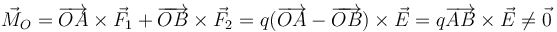
la acción de un par sobre un sólido es producir una rotación de este. El par se anulará cuando los dos vectores sean paralelos, momento en que la barra estará alineada con el campo.
6 Esfera cargada en volumen y superficie
Se tiene una distribución de carga formada por una esfera de radio b cargada uniformemente con una densidad volumétrica de carga ρ0, Esta esfera está forrada por una superficie esférica (también de radio b) con densidad de carga superficial σ0, de tal forma que la carga total del sistema es nula.
6.1 Pregunta 1
¿Cuánto vale σ0?
- A − ρ0b
- B − ρ0
- C − 4πb2ρ0
- D − ρ0b / 3
- Solución
La respuesta correcta es la D.
La carga total del sistema es
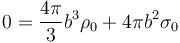
y despejando

6.2 Pregunta 2
Para esta distribución de carga, ¿cuánto vale el campo eléctrico que produce?
- A Es nulo en el interior de la esfera y vale
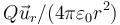 en el exterior con Q = (4πb3 / 3)ρ0.
en el exterior con Q = (4πb3 / 3)ρ0.
- B Es nulo en el interior de la esfera y vale
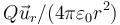 en el exterior con Q = (4πb2)σ0.
en el exterior con Q = (4πb2)σ0.
- C Es nulo en todos los puntos del espacio.
- D Es nulo en el exterior de la esfera y vale
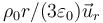 en el interior.
en el interior.
- A Es nulo en el interior de la esfera y vale
- Solución
La respuesta correcta es la D.
Por aplicación de la ley de Gauss, cualquier superficie interior a la esfera encerrará algo de carga y por tanto el flujo a través de ella no es nulo. Por tanto, el campo en el interior de la esfera es distinto de 0.
Esto ya descarta las respuestas A, B y C y deja solo la correcta, D.
Por la misma ley de Gauss puede hallarse el campo de esta distribución con simetría esférica y el resultado es un campo nulo en el exterior (ya que la carga encerrada es nula) y en el interior el mismo que el que produce una esfera cargada uniformemente en volumen (ya que la superficie esférica queda fuera).
6.3 Pregunta 3
Para este sistema, ¿cuánto vale el potencial eléctrico en el centro de la esfera?
- A
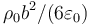 ,
,
- B Es nulo.
- C Tiende a infinito.
- D
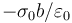 .
.
- A
- Solución
La respuesta correcta es la A.
El potencial eléctrico en el centro de la esfera no tiende a infinito, porque esto solo ocurre donde hay cargas puntuales y en este sistema no hay ninguna.
Tampoco es nulo porque el campo eléctrico siempre va en el sentido radial hacia afuera (dentro de la esfera) o es nulo (fuera de ella). Por tanto la integral desde el infinito hasta el centro de la esfera (que nos da el potencial del centro) será distinta de cero.
Puesto que el campo va de mayor a menor potencial y sabemos que en el interior de la esfera va hacia afuera, concluimos que el potencial en el centro es mayor que en el exterior (siendo 0 en el infinito). La única solución no nula y positiva es la A.
Por supuesto, también puede hallarse este potencial por integración directa a partir de las densidades de carga o integrando el campo eléctrico del apartado anterior.
Si se hace por integración directa sería
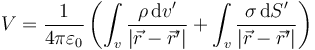
En el centro de la esfera 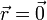 . Para los diferenciales de volumen tomamos coronas esféricas concéntricas
. Para los diferenciales de volumen tomamos coronas esféricas concéntricas
Esto nos da
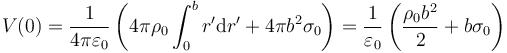
Sustituyendo aquí el valor de σ0

7 Campo de dos cargas
Una carga puntual de valor 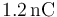 se encuentra situada en el punto
se encuentra situada en el punto 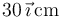 y una de valor
y una de valor 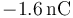 en
en 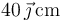 .
.
7.1 Pregunta 1
¿Cuánto vale, en módulo, el campo en 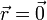 ?
?
- A 30 V/m
- B 150 V/m
- C 210 V/m
- D −30 V/m
- Solución
La respuesta correcta es la B.
El campo de un par de cargas puntuales en un punto 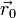 lo da la suma vectorial
lo da la suma vectorial
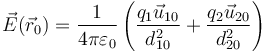
siendo di0 la distancia desde el punto donde se halla la carga i al punto donde queremos hallar el campo y 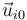 el unitario en la dirección de la recta de la carga al punto
el unitario en la dirección de la recta de la carga al punto 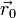 y en el sentido hacia que se aleja de la carga.
y en el sentido hacia que se aleja de la carga.
En este caso 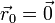 , lo que simplifica los cálculos. Sustituyendo los valores del enunciado
, lo que simplifica los cálculos. Sustituyendo los valores del enunciado

siendo su módulo
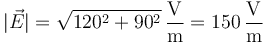
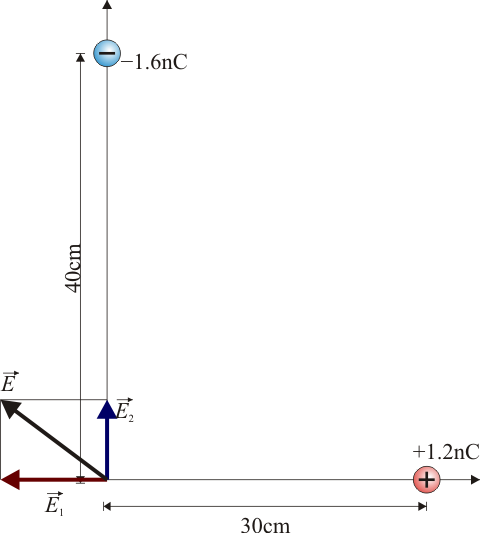
7.2 Pregunta 2
¿Y el potencial eléctrico en el mismo punto 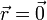 ?
?
- A
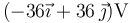
- B 72 V.
- C 210 V.
- D 0 V.
- A
- Solución
La respuesta correcta es la D.
Operando de la misma forma, el potencial en un punto dado es
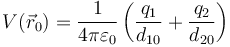
lo que nos da
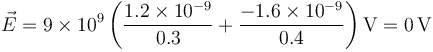
8 Definición de franklin
Un franklin es una unidad de carga eléctrica definida como aquella tal que dos cargas de 1 franklin situadas a 1 cm se ejercen una fuerza de 1 dina ( = 10 − 5N). ¿A cuantos culombios equivale un franklin?
- A
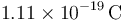
- B
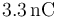
- C
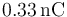
- D
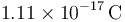
- A
- Solución
La respuesta correcta es la C.
Esta es una simple aplicación de la ley de Coulomb. La fuerza entre dos cargas iguales es, en módulo,
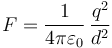
En este caso, empleando unidades del SI
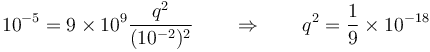
Tomando la raíz cuadrada
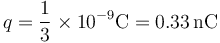
La respuesta correcta es por tanto la C.
9 Sentido del campo eléctrico
Dada una cierta distribución de potencial eléctrico, el campo eléctrico apunta en el sentido…
- A en que decrece el potencial.
- B tangente a las superficies equipotenciales.
- C en que crece o decrece el potencial, dependiendo de donde estén las cargas eléctricas.
- D en que crece el potencial.
- Solución
La respuesta correcta es la A.
10 Esferas concéntricas
Se tienen dos superficies esféricas concéntricas de radios a y 2a, centradas en el origen de coordenadas. La interior está cargada con una densidad superficial uniforme + σ0 y la exterior con una − σ0.
10.1 Pregunta 1
El campo eléctrico en un punto a 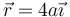 vale
vale
- A
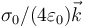
- B
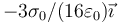
- C

- D
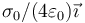
- A
- Solución
La respuesta correcta es la B.
Fuera de las dos esferas, el sistema se ve como dos cargas puntuales, pero al ser concéntricas, las dos cargas están el mismo punto, por lo que todo el sistema equivale en su exterior a una sola carga con el valor de la carga total del sistema
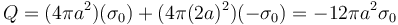
Puesto que esta carga es negativa, el campo que produce en el exterior va hacia adentro, lo cual ya nos dice que la respuesta correcta es la B.
El valor del campo que produce en  es
es
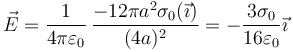
10.2 Pregunta 2
Para este sistema el potencial en el origen de coordenadas vale\ldots
- A
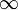
- B 0
- C
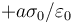
- D
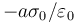
- A
- Solución
La respuesta correcta es la D.
El potencial debido a dos superficies esféricas de radios a y 2a, en su centro, es la suma del que produce cada una
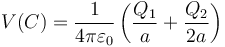
Sustituyendo los valores de las cargas
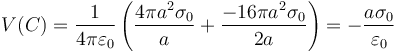
11 Fuerza sobre una carga en movimiento
Una carga puntual se mueve en el seno de un campo eléctrico 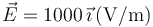 y de un campo magnético
y de un campo magnético 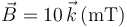 . ¿Con qué velocidad debe moverse la carga para que la fuerza electromagnética sobre ella sea nula?
. ¿Con qué velocidad debe moverse la carga para que la fuerza electromagnética sobre ella sea nula?
- A
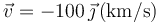
- B Es imposible que se anule la fuerza.
- C
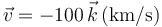
- D
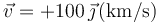
- A
- Solución
La respuesta correcta es la .
La fuerza sobre una carga puntual la da ley de Lorentz
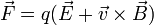
Para que esta fuerza sea nula debe cumplirse

o, lo que es lo mismo
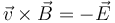
Esto implica que el campo eléctrico debe ser ortogonal al magnético. Como en este caso es así, es posible anularla y la respuesta B no es la correcta.
Asimismo, si la velocidad fuera paralela al campo magnético, el primer miembro se anularía, por lo que la respuesta C tampoco es posible. Comprobamos qué ocurre con las otras dos posibilidades. Para la A, empleando el SI,
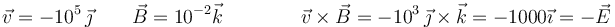
Con esta se cumple, por tanto, es la correcta. En el caso D nos hubiera dado con sentido contrario.
12 Acción de dos cargas sobre una tercera
Se tiene un sistema formado por tres cargas puntuales de valores + q, + q y + 2q situadas en las posiciones de la figura.
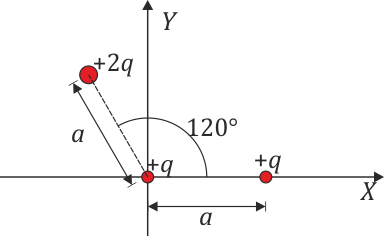
12.1 Pregunta 1
Si llamamos 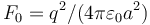 , la fuerza sobre la carga situada en el origen es igual a
, la fuerza sobre la carga situada en el origen es igual a
- A
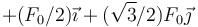
- B
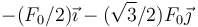
- C

- D
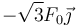
- A
- Solución
La respuesta correcta es la D.
Es simple suma vectorial. La carga que está en ele je OX ejerce una fuerza
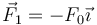
mientras que la carga 2q ejerce la fuerza
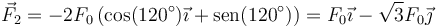
Sumando estos dos vectores la componente X se anula (lo cual, si se ve de entrada, resuelve directamente el problema) y queda
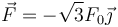
12.2 Pregunta 2
¿Qué trabajo es necesario realizar por un agente externo para llevar la carga cuasiestáticamente del origen de coordenadas hasta el infinito?
- A − 3F0a.
- B Es nulo.
- C Es infinito.
- D + 3F0a.
- Solución
La respuesta correcta es la A.
El trabajo para mover una carga en el campo de otras es igual a
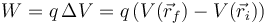
En este caso, el potencial en el punto final es nulo, mientras que el inicial es el debido a las otras dos cargas
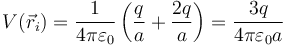
por lo que el trabajo vale
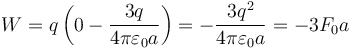
Es fácil ver que esta es la respuesta correcta sin hacer ningún cálculo, ya que las cargas positivas se repelen entre sí, por lo que la carga del origen ya tiende a irse sola al infinito. Por ello, el trabajo que hay que hacer es negativo, ya que al conseguir que la carga se mueva de forma cuasiestática hay que extraerle energía.





