No Boletín - Partícula motorizada en hélice (Ex.Ene/15)

De Laplace

Revisión a fecha de 18:25 5 mar 2015; Enrique (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Ley horaria
3 Componentes tangenciales de la aceleración
4 Triedro intrínseco
5 Fuerza motora y su trabajo en una vuelta de hélice
6 Componente vertical del momento cinético respecto al origen de coordenadas

1 Enunciado

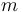Una partícula $P\,$ , de masa $m\,$ , se encuentra ensartada sin rozamiento en la hélice 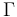$\Gamma\,$ de la figura. Esto permite que la posición de la partícula (respecto al triedro cartesiano 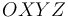$OXYZ\,$ ) pueda describirse mediante las ecuaciones $\theta\,$ -paramétricas de dicha hélice vincular:

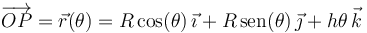
$\overrightarrow{OP}=\vec{r}(\theta)=R\,\mathrm{cos}(\theta)\,\vec{\imath}+R\,\mathrm{sen}(\theta)\,\vec{\jmath}+h\theta\,\vec{k}$

donde $R\,$ y $h\,$ son constantes positivas conocidas.

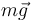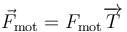Además de soportar la acción gravitatoria ( $m\vec{g}\,$ ) y la fuerza de reacción vincular ( $\vec{\Phi}\,$ ) ejercida por la hélice lisa, la partícula es empujada en sentido ascendente por una fuerza motora tangente al vínculo ( $\vec{F}_{\mathrm{mot}}=F_{\mathrm{mot}}\overrightarrow{T}\,$ ). 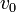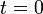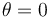Como resultado de todo ello, la partícula sube a lo largo de la hélice con celeridad constante $v_0\,$ , partiendo en el instante inicial ( $t=0\,$ ) desde la posición $\theta=0\,$ .

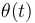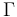Halle la ley horaria $\theta(t)\,$ con la que la partícula $P\,$ recorre la hélice $\Gamma\,$ .
Calcule (en función de $\theta\,$ ) las componentes tangencial y normal de la aceleración de la partícula $P\,$ , así como los vectores tangente unitario y normal principal del triedro intrínseco de su trayectoria.
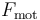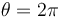Proyectando la ecuación de la segunda ley de Newton sobre la dirección tangente a la hélice, determine el módulo de la fuerza motora ( $F_{\mathrm{mot}}\,$ ) que actúa sobre la partícula $P\,$ . ¿Qué trabajo total realiza dicha fuerza motora entre el instante inicial y el instante en el que la partícula $P\,$ alcanza la posición $\theta=2\pi\,$ ?
Calcule la componente vertical del momento cinético de la partícula $P\,$ respecto al origen de coordenadas $O\,$ , y explique por qué dicha componente resulta independiente del tiempo.

2 Ley horaria

Se calcula el vector velocidad instantánea de la partícula derivando su vector de posición respecto al tiempo:

$\vec{v}\,=\,\displaystyle\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}\,=\,\dot{\theta}\,\displaystyle\frac{\mathrm{d}\vec{r}}{\mathrm{d}\theta}\,=\,\dot{\theta}\,\left[-R\,\mathrm{sen}(\theta)\,\vec{\imath}+R\,\mathrm{cos}(\theta)\,\vec{\jmath}+h\,\vec{k}\,\right]$

Igualando a 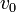$v_0\,$ el módulo de este vector (dado que sabemos que la partícula recorre la hélice con celeridad constante 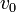$v_0\,$ ), se deduce que $\dot{\theta}$ es constante:

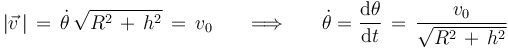
$|\vec{v}\,|\,=\,\dot{\theta}\,\sqrt{R^2\,+\,h^2}\,=\,v_0\,\,\,\,\,\,\,\,\,\,\Longrightarrow\,\,\,\,\,\,\,\,\,\, \dot{\theta}=\frac{\mathrm{d}\theta}{\mathrm{d}t}\,=\,\frac{v_0}{\sqrt{R^2\,+\,h^2}}$

Separando variables e integrando entre 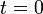$t=0\,$ y un instante genérico $t\,$ , obtenemos la ley horaria solicitada:

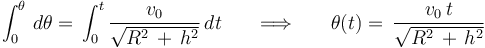
$\int^{\theta}_{0}\,d\theta=\,\int^{t}_{0} \displaystyle\frac{v_0}{\sqrt{R^2\,+\,h^2}}\,dt\,\,\,\,\,\,\,\,\,\,\Longrightarrow\,\,\,\,\,\,\,\,\,\, \theta(t)=\,\displaystyle\frac{v_0\, t}{\sqrt{R^2\,+\,h^2}}$

3 Componentes tangenciales de la aceleración

Conocida la ley horaria, es posible expresar el vector velocidad instantánea de la partícula en función del tiempo:

$\vec{v}(t)\,=\,\frac{v_0}{\sqrt{R^2\,+h^2}}\left[-R\,\,\mathrm{sen}\left(\frac{v_0\,t}{\sqrt{R^2\,+h^2}}\right)\vec{\imath}+R\,\,\mathrm{cos}\left(\frac{v_0\,t}{\sqrt{R^2\,+h^2}}\right)\vec{\jmath}+h\,\vec{k}\,\right]$

Derivando respecto al tiempo, obtenemos el vector aceleración instantánea de la partícula:

$\vec{a}(t)\,=\,\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}\,=\,\frac{R\, v_0^2}{R^2\,+h^2}\left[-\mathrm{cos}\left(\frac{v_0\,t}{\sqrt{R^2\,+h^2}}\right)\vec{\imath}-\mathrm{sen}\left(\frac{v_0\,t}{\sqrt{R^2\,+h^2}}\right)\vec{\jmath}\,\right]$

Pero la partícula tiene celeridad constante, y por tanto la componente tangencial de su aceleración es nula:

$a_t\,=\,\dot{v}\,=\,0$

Esto implica que toda la aceleración de la partícula es aceleración normal:

$\overrightarrow{a_t}\,=\,\vec{0}\,\,\,\,\,\,\,\,\,\,\Longrightarrow\,\,\,\,\,\,\,\,\,\,\overrightarrow{a_n}\,=\,\vec{a}$

Y entonces, la componente normal de la aceleración (que siempre es positiva y por eso se llama centrípeta) coincide con el módulo del vector aceleración instantánea:

$a_n\,=\,|\overrightarrow{a_n}|\,=\,|\vec{a}\,|\,=\,\frac{R\, v_0^2}{R^2\,+h^2}$

4 Triedro intrínseco

El vector tangente unitario se obtiene normalizando el vector velocidad instantánea:

$\overrightarrow{T}\,=\,\frac{\vec{v}}{|\vec{v}\,|}\,=\,\frac{\vec{v}}{v_0}\,=\,\frac{1}{\sqrt{R^2\,+h^2}} \,\left[-R\,\mathrm{sen}(\theta)\,\vec{\imath}+R\,\mathrm{cos}(\theta)\,\vec{\jmath}+h\,\vec{k}\,\right]$

El vector normal principal se obtiene normalizando el vector aceleración normal (que en este caso coincide con el vector aceleración instantánea):

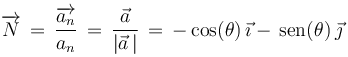
$\overrightarrow{N}\,=\,\frac{\overrightarrow{a_n}}{a_n}\,=\,\frac{\vec{a}}{|\vec{a}\,|}\,=\,-\,\mathrm{cos}(\theta)\,\vec{\imath}-\,\mathrm{sen}(\theta)\,\vec{\jmath}$

Aunque el ejercicio no nos lo pide, es fácil obtener también el vector binormal:

$\overrightarrow{B}\,=\,\overrightarrow{T}\times\overrightarrow{N}\,=\, \frac{1}{\sqrt{R^2\,+h^2}} \,\left[h\,\mathrm{sen}(\theta)\,\vec{\imath}-h\,\mathrm{cos}(\theta)\,\vec{\jmath}+R\,\vec{k}\,\right]$

5 Fuerza motora y su trabajo en una vuelta de hélice

Sobre la partícula actúan tres fuerzas: el peso (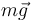 $m\vec{g}\,$ ), la fuerza motora ( 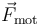$\vec{F}_{\mathrm{mot}}\,$ ) y la fuerza de reacción vincular ( $\vec{\Phi}\,$ ). La segunda ley de Newton establece que:

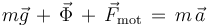
$m\vec{g}\,+\,\vec{\Phi}\,+\,\vec{F}_{\mathrm{mot}}\,=\,m\,\vec{a}$

Proyectando esta ecuación sobre la dirección tangente a la hélice, es decir, multiplicándola escalarmente por el vector 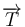$\overrightarrow{T}\,$ , se obtiene:

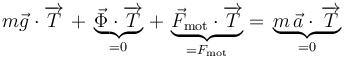
$m\vec{g}\cdot\overrightarrow{T}\,+\,\underbrace{\vec{\Phi}\cdot\overrightarrow{T}}_{=0}\,+\,\underbrace{\vec{F}_{\mathrm{mot}}\cdot\overrightarrow{T}}_{=F_{\mathrm{mot}}}=\,\underbrace{m\,\vec{a}\cdot\,\overrightarrow{T}}_{=0}$

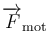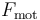donde se ha tenido en cuenta que el vínculo es liso ( $\vec{\Phi}\,$ es ortogonal a la hélice y por tanto no tiene componente tangencial), que la fuerza motora es tangente al vínculo y de sentido ascendente (la componente tangencial de $\overrightarrow{F}_{\mathrm{mot}}\,$ coincide con su módulo $F_{\mathrm{mot}}\,$ ), y que el movimiento es uniforme (la partícula no tiene aceleración tangencial). Despejando el módulo de la fuerza motora, se llega a:

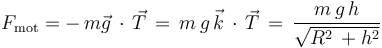
$F_{\mathrm{mot}}=-\,m\vec{g}\,\cdot\,\vec{T}\,=\,m\,g\,\vec{k}\,\cdot\,\vec{T}\, =\,\frac{m\,g\,h}{\sqrt{R^2\,+h^2}}$

\noindent El trabajo que realiza la fuerza motora se puede obtener aplicando el teorema de la energía cinética o de las fuerzas vivas, este teorema nos dice que el trabajo realizado por todas las fuerzas que actúan sobre la partícula es igual a la variación de la energía cinética, como la partícula se mueve con celeridad constante entonces no hay variación de la energía cinética

\[ W_{tot}\,=W_{mg}\,+W_{F_{mot}}\,+W_{\Phi}\,=\Delta K\,=0 \]

\noindent Despejando y teniendo en cuenta que la fuerza de reacción vincular no realiza trabajo por ser el vínculo liso y que el peso es un fuerza conservativa,

\[ \fbox{$W_{F_{mot}}$}\,=-\,W_{mg}\,=\Delta U\,=\,m g \biggl( z(\theta=2\pi)\,-\,z(\theta=0)\biggr)\,=\fbox{$2\,\pi\,m\,g\,h$} \]

\newpage

\noindent También se puede calcular directamente el trabajo realizado por la fuerza motora

\[ W_{F_{mot}}\,=\int^{^{2\pi}}_{0}\,\vec{F}_{\mbox{\footnotesize mot}}\,\cdot\,d\vec{r}\,=\int^{^{2\pi}}_{0}\,\vec{F}_{\mbox{\footnotesize mot}}\,\cdot\,\vec{v}\,dt\,=F_{\mbox{\footnotesize mot}}\,v_0\,\int^{^{t_f}}_{0}\,dt\,=F_{\mbox{\footnotesize mot}}\,v_0\,t_f \]

\noindent donde el valor de $t_f$ se obtiene a partir de la ley horaria, $\,\,t_f\,=\displaystyle\frac{2\pi\,\sqrt{R^2\,+h^2}}{v_0}$.

6 Componente vertical del momento cinético respecto al origen de coordenadas

No Boletín - Partícula motorizada en hélice (Ex.Ene/15)

De Laplace

Contenido

1 Enunciado

2 Ley horaria

3 Componentes tangenciales de la aceleración

4 Triedro intrínseco

5 Fuerza motora y su trabajo en una vuelta de hélice

6 Componente vertical del momento cinético respecto al origen de coordenadas

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES