Partícula sobre espiral con muelle, Enero 2015 (G.I.C.)
De Laplace
1 Enunciado
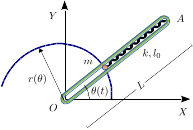
Una partícula de masa m está engarzada en la barra ranurada de la figura. El muelle, de longitud natural l0 < L y constante elástica k, la empuja de modo que, al girar la barra, la partícula está obligada a moverse sobre la espiral indicada, de ecuación r(θ) = r0eθ, con θ = θ(t). La barra gira de modo que la partícula se mueve con rapidez constante v0. El efecto de la gravedad es despreciable.
- Usando coordenadas polares, escribe las expresiones del vector de posición, velocidad y aceleración de la partícula. Deja el resultado en función de θ y sus derivadas.
- Calcula la ley horaria θ(t).
- Determina la fuerza que ejerce el muelle sobre la partícula, así como la energía potencial del muelle. Expresa estos dos resultados en función del ángulo θ.
- ¿Se conserva la energía mecánica de la partícula? ¿Y el momento cinético respecto a O? Razona las respuestas.
2 Solución
2.1 Vectores en polares
La posición de un punto cualquiera situado en un plano en polares viene determinada por el par de coordenadas (r,θ), donde r es la distancia al origen y θ es el ángulo que forma  con el eje OX. El vector de posición en la base polar es
con el eje OX. El vector de posición en la base polar es
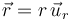
En este caso, la partícula está obligada a moverse sobre una espiral. Esto se especifica imponiendo una relación entre las coordenadas r y θ. Según el enunciado r = r0eθ, con θ = θ(t). Para este caso, el vector de posición es

La velocidad es la derivada de este vector respecto del tiempo. En polares, hay que tener en cuenta que los vectores de la base dependen del tiempo. Tenemos aquí dos funciones que dependen del tiempo: θ(t) y 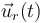 . Tenemos que aplicar la regla de Leibniz
. Tenemos que aplicar la regla de Leibniz
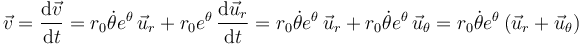
Hemos utilizado 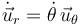 .
.
El enunciado nos dice que la rapidez de la partícula es constante e igual a v0. Tenemos entonces

Y la velocidad queda

Derivamos de nuevo respecto al tiempo para obtener la aceleración.
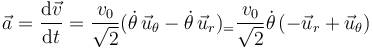
Observemos que  y
y  son perpendiculares, es decir, la aceleración tangencial es nula. Esto es coherente con el hecho de que la rapidez de la partícula sea constante.
son perpendiculares, es decir, la aceleración tangencial es nula. Esto es coherente con el hecho de que la rapidez de la partícula sea constante.