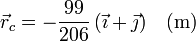Entrar Página Discusión Historial Go to the site toolbox

Centro de masas de cuatro partículas en un cuadrado

De Laplace

Contenido

1 Enunciado

Se tienen 4 masas que ocupan los vértices de un cuadrado de lado 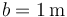b=1\,\mathrm{m}. Calcule la posición del centro de masas del sistema en cada uno de los casos siguientes

  1. m_1=m_2=m_3=m_4=1\,\mathrm{kg}.
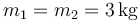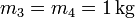  2. m_1=m_2=3\,\mathrm{kg}, m_3=m_4=1\,\mathrm{kg}.
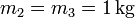  3. m_1=m_4=3\,\mathrm{kg}, m_2=m_3=1\,\mathrm{kg}.
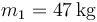  4. m_1=47\,\mathrm{kg}, m_2=m_3=m_4=1\,\mathrm{kg}.

2 Introducción

Para un sistema de n masas puntuales, cada una con una masa mi y un vector de posición 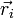\vec{r}_i, la posición del centro de masas (CM) viene dada por la expresión

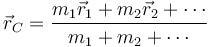
\vec{r}_C = \frac{m_1\vec{r}_1+m_2\vec{r}_2+\cdots}{m_1+m_2+\cdots}

En este caso tenemos cuatro masas. Utilizando el sistema de ejes de la figura sus vectores de posición son

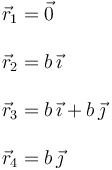
\begin{array}{l} \displaystyle \vec{r}_1 = \vec{0}\\ \\ \displaystyle \vec{r}_2 = b\,\vec{\imath}\\ \\ \displaystyle \vec{r}_3 = b\,\vec{\imath} +b\,\vec{\jmath}\\ \\ \displaystyle \vec{r}_4 = b\,\vec{\jmath} \end{array}

Aplicando la expresión que nos da el CM tenemos

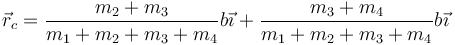
\displaystyle \vec{r}_{c} = \frac{m_2+m_3}{m_1+m_2+m_3+m_4}b\vec{\imath}+\frac{m_3+m_4}{m_1+m_2+m_3+m_4}b\vec{\imath}

Examinemos cada uno de los casos planteados.

3 Todas las masas iguales

En esta situación obtenemos

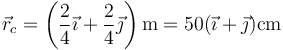
\vec{r}_{c}=\left(\frac{2}{4}\vec{\imath}+\frac{2}{4}\vec{\jmath}\right)\mathrm{m}=50(\vec{\imath}+\vec{\jmath})\mathrm{cm}

El CM se halla en el centro del cuadrado.

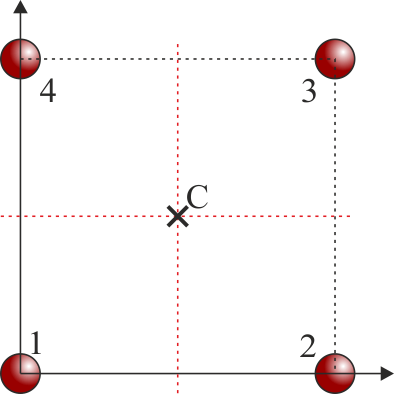
Imagen:Cuatro-masas-iguales.png

En un sistema que tenga un plano de simetría, el CM se encuentra sobre éste. En el caso del cuadrado con las cuatro masas iguales tenemos diferentes planos de simetría, por ejemplo dos rectas paralelas a los ejes por el centro. El CM se encuentra en la intersección de estas. Igualmente podríamos haber considerado la intersección de las dos diagonales.

4 Masas iguales contiguas

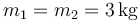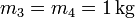Si m_1=m_2=3\,\mathrm{kg}, y m_3=m_4=1\,\mathrm{kg}, aplicando la expresión tenemos

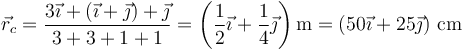
\displaystyle \vec{r}_c = \frac{3\vec{\imath}+(\vec{\imath}+\vec{\jmath})+\vec{\jmath}}{3+3+1+1}= \left(\frac{1}{2}\vec{\imath}+\frac{1}{4}\vec{\jmath}\right)\mathrm{m}=\left(50\vec{\imath}+25\vec{\jmath}\right)\,\mathrm{cm}

En este caso el CM se encuentra por debajo del centro del cuadrado.

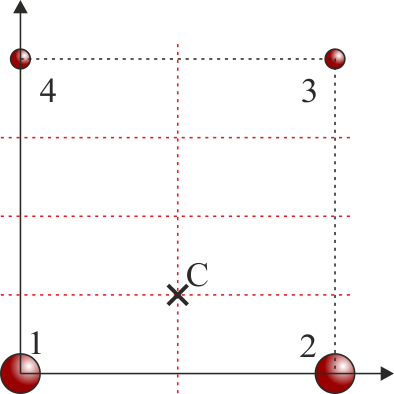
Imagen:Cuatro-masas-iguales-contiguas.png

La vertical que pasa por el centro del cuadrado sigue siendo un eje de simetría, por lo que el CM se encuentra en él, pero la horizontal ya no lo es.

Las masas más pesadas “tiran” del CM hacía ellas. En este caso, que las masas inferiores cuentan el triple que las superiores, la distancia vertical del CM a las inferiores es 1/3 de la distancia a las superiores.

5 m1=m4 y m2=m3

Aplicando la expresión tenemos

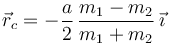
\displaystyle \vec{r}_c = -\frac{a}{2}\,\frac{m_1-m_2}{m_1+m_2}\,\vec{\imath}

El eje X es de simetría, luego el CM debe estar en él. Además, las masas m1 y m4 son más grandes, por lo que el CM está más cerca de ellas. Sustituyendo los valores numéricos tenemos

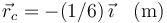
\vec{r}_c = -(1/6)\,\vec{\imath}\quad(\mathrm{m})

Este caso es equivalente al anterior si giramos el cuadrado 90°.

6 m2=m3=m4

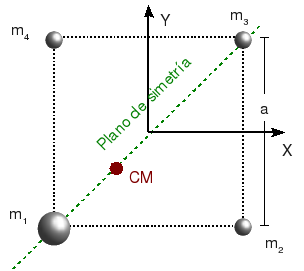
Aplicando la expresión tenemos

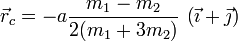
\displaystyle \vec{r}_c = -a\frac{m_1-m_2}{2(m_1+3m_2)}\,\left(\vec{\imath}+\vec{\jmath}\right)

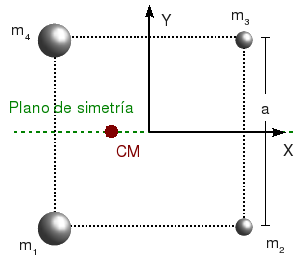
En este caso el eje de simetría es la diagonal que se muestra en la figura. El CM debe estar en esa diagonal, y más cerca de la masa m1 pues esta es mucho mayor que las otras. Sustituyendo los valores numéricos tenemos

\vec{r}_c = -\dfrac{99}{206}\,(\vec{\imath}+\vec{\jmath})\quad(\mathrm{m})

Obtenido de "http://tesla.us.es/wiki/index.php/Centro_de_masas_de_cuatro_part%C3%ADculas_en_un_cuadrado"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace