Motocicleta que acelera
De Laplace
1 Enunciado
Es conocido que al arrancar un coche, éste levanta un poco el morro y se hunde por la parte trasera El mismo principio se aplica a los caballitos de las motocicletas. Supongamos un automóvil con una masa M y tal que su centro de masas se encuentra a una altura H respecto a los ejes de las ruedas (las cuales tienen radio R y masa mR). El CM está a una distancia dA del eje celantero y a una dB del trasero.
- Calcule la fuerza que se ejerce sobre cada eje cuando el coche arranca con una aceleración a0 sobre un suelo horizontal.
- Determine la fuerza de rozamiento que el suelo ejerce sobre cada rueda. ¿Cuál es el mínimo valor que debe tener el coeficiente de rozamiento para que el coche pueda arrancar?
- Si a0 < 0, es decir, si el coche está frenando, ¿cuánto valen las fuerzas normales sobre cada eje? ¿Y las tangenciales? ¿Y las de rozamiento sobre las ruedas?
2 Cálculo de las fuerzas
Es evidente que al acelerar horizontalmente, se va a ejercer una fuerza horizontal sobre cada eje. Lo que ya no es tan evidente es que como resultado de esta aceleración se ejerza también una fuerza normal, que además es diferente sobre cada uno.
La razón es que a la hora de considerar el movimiento de un sólido, no solo hay que tener en cuenta la resultante de las fuerzas aplicadas, sino también las de los momentos.
Sobre el cuerpo del coche se ejercen tres fuerzas:
- Su peso
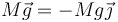
- La fuerza que ejerce el eje delantero,
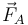
- la fuerza que ejerce el eje trasero,
A su vez, las fuerzas ejercidas por los dos ejes se pueden descomponer en una componente vertical y una horizontal

El centro de masas (como el resto del cuerpo del coche) adquiere una aceleración horizontal
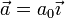
por lo que la segunda ley de Newton nos da, para el balance de fuerzas sobre el sistema,
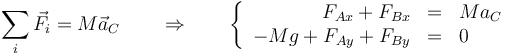
Por otro lado, en la situación en que el coche no cabecea (suponemos una suspensión muy rígida), la suma de los momentos respecto al centro de masas debe anularse
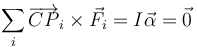
De las cinco fuerzas que actúan sobre el sistema (considerando las de cada eje como dos, una horizontal y una vertical) hay una aplicada sobre el propio CM, por lo que su momento es nulo. Los brazos de las otras cuatro son las distancias horizontales o verticales de sus rectas soporte al CM. De estas cuatro, tres producen un giro positivo y solo una negativo, de forma que tenemos
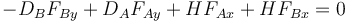
Despejando y sustituyendo la ecuación para la aceleración del CM nos queda el sistema
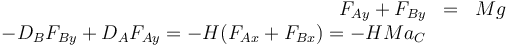
con solución

Vemos que para aceleración positiva, la fuerza que ejerce el eje delantero es menor que la del trasero (y por la tercera ley de Newton, lo mismo se cumplirá para la fuerza que el coche ejerce sobre los ejes). Esto es lo que provoca que el coche cabecee, hundiéndose por la parte trasera.
Si la aceleración es lo suficientemente grande puede anularse completamente la fuerza sobre el eje delantero, y por tanto, levantar el vehículo por su morro. Esto es lo que consigue un motorista al hacer un caballito.
Puesto que se trata de anular la cantidad gDB − aCH hay tres formas de conseguirlo, que se pueden aplicar simultáneamente: aumentar la aceleración, aumentar la altura del centro de masas, H, y reducir la distancia al eje trasero, DB. Esto lo consigue el motorista erguiéndose y echándose hacia atrás en la moto.





