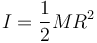Momento de inercia de diversos sistemas continuos (GIC)
De Laplace
Contenido |
1 Enunciado
Calcula el momento de inercia en los siguientes sistemas
- Un aro circular homogéneo de masa M y radio R respecto a un eje perpendicular que pase por su centro de masas.
- Una varilla homogénea de masa M y longitud L respecto a un eje perpendicular a ella que pase por su centro.
- Una varilla homogénea de masa M y longitud L respecto a un eje perpendicular a ella que pase por uno de sus extremos.
- Un disco homogéneo de masa M y radio R respecto a un eje perpendicular a él que pase por su centro.
2 Solución
2.1 Aro circular
El momento de inercia de un sistema continuo de masa respecto a un eje es
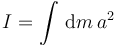
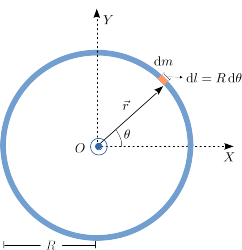
donde a es la distancia de cada punto del cuerpo hasta el eje. La figura de la derecha muestra el aro. El eje respecto al que queremos calcular el momento de inercia es perpendicular a él y pasa por el punto O.
Descomponemos el aro en pequeños trocitos diferenciales de masa. Cada uno de estos trocitos tiene una masa
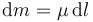
donde μ es la densidad lineal de masa y dl es la longitud del trocito. Como el aro es homogéneo su densidad lineal de masa es la masa total dividida por la longitud del aro
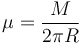
Como ya hemos visto otras veces, la longitud del trocito se puede expresar como
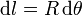
siendo dθ el ángulo subtendido por el trocito.
Vemos en el dibujo que todos los dm están a la misma distancia del punto O, es decir,
a = R
Entonces el momento de inercia es
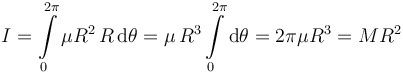
En este caso también se podría haber razonado así
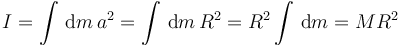
En el último paso hemos dicho que 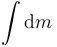 es la suma de todas las masas diferenciales, es decir, la masa total del aro.
es la suma de todas las masas diferenciales, es decir, la masa total del aro.
2.2 Varilla respecto a un eje que pasa por su centro
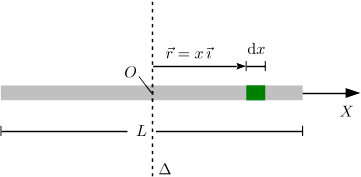
La figura muestra la configuración que estudiamos a continuación. En este caso, los diferenciales de masa está a distancias diferentes. Tenemos
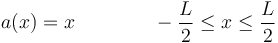
La longitud de cada diferenciales de masa es
dl = dx
Como la varilla es homogénea la densidad lineal de masa es
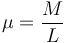
Entonces el momento de inercia es
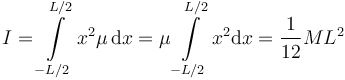
2.3 Varilla respecto a un eje que pasa por su extremo
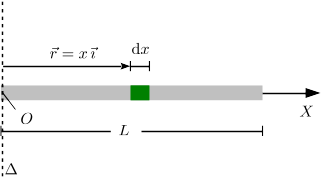
Esta configuración es similar a la anterior. La única diferencia es que, al estar el eje en el extremo izquierdo, el rango de variación de la coordenada x es distinto.

La longitud de cada diferenciales de masa es
dl = dx
Como la varilla es homogénea la densidad lineal de masa es
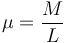
Entonces el momento de inercia es
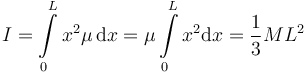
2.3.1 Resolución utilizando el teorema de Steiner
Este resultado también se puede obtener a partir del caso anterior utilizando el teorema de Steiner.
Iext = ICM + Md2
donde d es la distancia desde el eje en el extremo hasta el centro de masas. En este caso tenemos
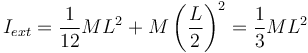
Si comparamos estos dos casos, el momento de inercia es mayor cuando el eje de giro está en el extremo. Esto quiere decir que es más difícil hacer girar la barra en este caso que si el eje pasa por su centro. Cuando el eje pasa por el extremo las masas de la barra están mas lejos del eje de giro, por lo que la inercia al giro es mayor.
2.4 Disco homogéneo respecto a un eje perpendicular que pasa por su centro
Ahora consideramos un sistema plano, es decir, con una distribución superficial de masa. La idea es similar, ahora consideramos el disco compuesto por pequeños diferenciales de superficie, cada uno con una masa
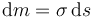
donde σ es la densidad superficial de masa. Si el disco es homogéneo esta densidad es la misma en todos los puntos y vale
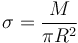
El momento de inercia sería
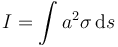
Esta integral sería mas fácil de calcular usando coordenadas cilíndricas. Sin embargo, vamos a hacer el cálculo de otra manera. El momento de inercia es una integral definida, es decir, una suma. Los sumandos son las contribuciones de todos los ds que se pueden escoger sobre el disco. Aplicamos la propiedad distributiva de la suma y la separamos la suma total en subsumas. Cada subsuma es la contribución de los ds que forma un aro, como se ve en la figura. Cada aro tiene un radio r y un grosor dr.
En el primer apartado calculamos el momento de inercia de un aro de radio R y masa total M. Reutilizando ese resultado aquí, tenemos que el momento de inercia de este aro diferencial es
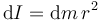
La masa del aro diferencial es dm = σds, donde σ es la densidad superficial de masa. Tenemos que calcular ds. Como 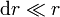 , podemos ignorar la curvatura del aro, y calcular su área como si fuera un rectángulo de base 2πr y altura dr, es decir
, podemos ignorar la curvatura del aro, y calcular su área como si fuera un rectángulo de base 2πr y altura dr, es decir
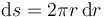
Esto es similar a calcular el volumen de un edificio muy grande multiplicando su base por su altura. Al hacer esto, despreciamos el hecho de que la base del edificio no es recta, sino que debe seguir la curvatura de la Tierra. Pero si la altura del edificio es muy pequeña comparada con el radio de la Tierra, podemos despreciar la curvatura de su base, y tratarla como si fuese plana.
Con esto, el momento de inercia del aro es
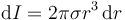
Para calcular el momento de inercia total sumamos la contribución de todos los aros que podemos definir sobre el disco, es decir
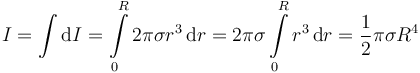
Como el disco es homogéneo, σ = M / πR2, por lo que el momento de inercia es