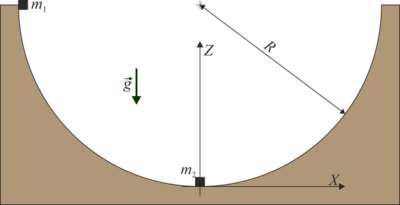
Colisión en el interior de un cuenco

De Laplace

1 Enunciado

En el interior de un cuenco hemisférico de radio 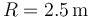cuyo borde es horizontal, se encuentran dos partículas que pueden deslizar sin rozamiento por su superficie. Una de ellas, de masa 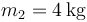, se encuentra en reposo en el fondo del cuenco. La otra, de masa 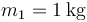se coloca en el borde del cuenco y desde allí se suelta.

1. Calcule, con justificación, la velocidad que lleva la masa 1 justo antes de impactar con la masa 2. Halle la reacción del cuenco sobre la masa 1 para el mismo instante.
2. Si el choque es perfectamente elástico, calcule las velocidades de las dos masas justo tras la colisión.
3. Para este caso elástico, halle la altura máxima desde el fondo del cuenco que alcanza cada una de las masas tras el choque.
4. Repita los dos apartados anteriores para el caso de que la colisión sea completamente inelástica. ¿Cuánta energía se pierde en la colisión en ese caso?

Tómese g = 9.8m/s²

2 Velocidad antes del impacto

3 Velocidades tras el impacto

4 Alturas máximas

5 Choque completamente inelástico

5.1 Velocidad tras la colisión

5.2 Altura máxima

5.3 Balance energético