Colisión inelástica en el plano
De Laplace
Contenido |
1 Enunciado
Un neutrón de masa m que se mueve con velocidad 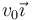 choca con un protón (de casi la misma masa), que se mueve con velocidad
choca con un protón (de casi la misma masa), que se mueve con velocidad 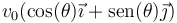 . La colisión es completamente inelástica, de forma que tras ella, las dos partículas se mueven solidariamente como un núcleo de deuterio. La colisión se produce en el origen de coordenadas.
. La colisión es completamente inelástica, de forma que tras ella, las dos partículas se mueven solidariamente como un núcleo de deuterio. La colisión se produce en el origen de coordenadas.
- ¿Cuál es la velocidad final de la nueva partícula formada? ¿Qué ángulo forma con el eje OX?
- ¿Cuánta energía se pierde en la colisión? ¿Para qué valores de θ es máxima o mínima esta energía perdida?
2 Velocidad final
Cuando la colisión es completamente inelástica, las dos partículas se fusionan en una, de masa la suma de las iniciales. La velocidad final se obtiene a partir de la conservación de la cantidad de movimiento.
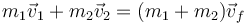
En este caso, que las dos partículas tienen la misma masa, la velocidad final es simplemente
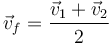
Sustituyendo los valores del enunciado

Usando las relaciones trigonométricas del ángulo mitad esto se puede escribir
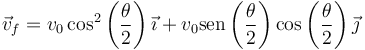
y sacando factor común