Osciladores no lineales. Péndulo simple (GIE)

De Laplace

1 Oscilaciones lineales. El oscilador armónico

El oscilador armónico es un modelo teórico que se aplica en primer lugar al comportamiento de sólidos elásticos, que verifican la ley de Hooke, pero cuya validez se extiende a muchísimos otros sistemas mecánicos (y físicos, en general, ya que es esencial en la teoría de circuitos en los campos electromagnéticos). La razón de su universalidad es que se trata del oscilador más sencillo posible: aquél en que la fuerza es lineal con la posición.

1.1 Ley de Hooke

Restringiéndonos al caso unidimensional, la ley de Hppke nos dice que la fuerza producida por un resorte elástico sobre una partícula es de la forma

siendo x_eq la posición de equilibrio para la cual esta fuerza es nula.

La ley de Hooke describe una fuerza recuperadora:

• cuando x > x_eq, la fuerza es negativa, lo cual quiere decir que tiende a reducir x.

• cuando x < x_eq, la fuerza es positiva, es decir, tiende a aumentar x.

Gráficamente, si representamos la fuerza como función de la longitud del resorte, el resultado es una recta de pendiente − k, es decir,

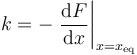
Esta recta pasa por F = 0 en la posición de equilibrio.

1.2 Energía potencial

1.3 Frecuencia de las oscilaciones

2 Oscilador no lineal

2.1 Posiciones de equilibrio

2.2 Aproximación lineal y parabólica

2.3 Frecuencia aproximada

2.4 Dependencia con la amplitud

3 El péndulo simple

3.1 Ecuación de movimiento del péndulo

3.2 Aproximación de ángulo pequeño

3.3 Ley del péndulo

3.4 Dependencia con la amplitud