Plano inclinado bidimensional, Noviembre 2013 (G.I.C.)

De Laplace

1 Enunciado

Una partícula de masa m desliza sin rozamiento sobre un plano inclinado un ángulo α sobre la horizontal. La partícula parte desde el origen con una velocidad paralela a la base del plano y módulo v₀, como se indica en la figura.

1. Dibuja el diagrama de cuerpo libre de la partícula.
2. Determina la velocidad de la partícula en cada instante.
3. Determina la posición de la partícula en cada instante.
4. Calcula el tiempo que tarda en llegar a la base del plano inclinado.
5. ¿Qué tipo de curva describe la partícula?

2 Solución

2.1 Diagrama de fuerzas

Las fuerzas que actúan sobre la partícula son el peso y la fuerza de reacción vincular del plano. Esta fuerza es perpendicular al plano, pues no hay rozamiento. La figura a la derecha muestra estas fuerzas.

2.2 Velocidad de la partícula

Para determinar la velocidad hemos de calcular la aceleración de la partícula en cada instante. Para ellos expresamos las fuerzas en los ejes de la figura anterior. Tenemos

Coma la partícula no se separa del plano la velocidad no tiene componente en el eje Y, pero sí puede tenerla en el eje Z que se muestra en la figura del enunciado. Por tanto la velocidad en cada instante es de la forma

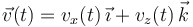
Derivando respecto al tiempo obtenemos la aceleración