Cuatro conductores paralelos
De Laplace
Revisión a fecha de 21:40 5 sep 2014; Antonio (Discusión | contribuciones)
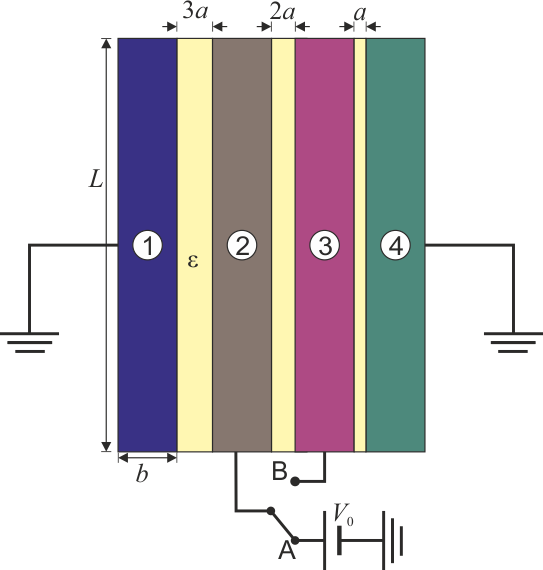
Se tiene un sistema de conductores en forma de bloques prismáticos cuadrados de lado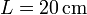 
de lado y grosor 
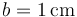. Estos bloques se sitúan paralelamente de forma que entre el primero y el segundo hay un espacio 3a; entre el 2º y el 3º hay 2a y entre el 3\tss{o} y el 4º: hay a, siendo 
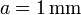. El espacio entre los conductores está lleno de un dieléctrico ideal de permitividad 
.
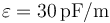El conductor 1 y el 4 se encuentran permanentemente a tierra.
Inicialmente el interruptor se encuentra en la posición A, de forma que el conductor 2 se encuentra a un potencial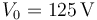 
$, mientras que el 3 está aislado y descargado.
- Calcule el potencial del conductor 3, así como las cargas netas en cada uno de los cuatro conductores.
- Halle el campo eléctrico en cada uno de los espacios entre conductores, y las cargas almacenadas en cada una de las superficies conductoras
- Suponga que bruscamente se pasa el interruptor de la posición A a la B, conectando los conductores 2 y 3, ¿cómo quedan en ese caso las cargas y potenciales de los diferentes conductores, así como las cargas de cada una de las superficies?
- Halle la energía almacenada en el sistema antes y después de mover el interruptor.
¿Cuánta energía se disipa en el proceso?, ¿cómo puede haber desaparecido esta energía?
Contenido |
