Dos esferas conductoras dentro de otra
De Laplace
Contenido |
1 Enunciado
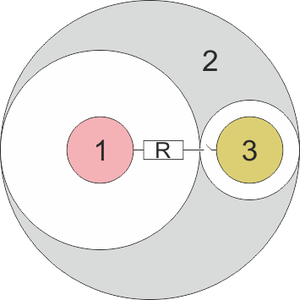
Se tiene un sistema de tres conductores esféricos. Uno de ellos (“2”) es una esfera de radio 54 mm con dos huecos esféricos, de radios 36 mm y 18 mm. En el centro de cada hueco se encuentran sendas esferas metálicas de radio 12 mm, siendo “1” la que está en el hueco grande y “3” la que está en el pequeño. Entre las esferas hay vacío y no hay más conductores ni cargas en el sistema.
Inicialmente la esfera “1” contiene una carga 120 nC mientras que los otros dos conductores están aislados y descargados.
- Halle el potencial de cada conductor, así como la energía almacenada en el sistema.
- Se conectan las dos esferas interiores mediante un hilo de resistencia 1 kΩ. Una vez que se ha vuelto a alcanzar el estado final, ¿cuáles son los nuevos potenciales de los conductores?
- ¿Cuál es la nueva energía almacenada? ¿Cuánta energía se ha disipado en la resistencia?
- Halle la potencia instantánea disipada en el cable justo tras la conexión.
Tómese
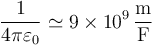
2 Potenciales antes de la conexión
La forma más sencilla de resolver este problema es mediante la construcción de un circuito equivalente.
En este caso, tenemos tres condensadores:
- Uno esférico entre la esfera 1 y la pared del hueco de 2, de capacidad
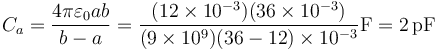
- Otro esférico entre la esfera 3 y la pared del hueco de 2, de capacidad
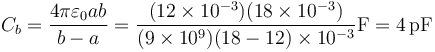
- Uno entre la superficie exterior del conductor 2 y el infinito, que se puede calcular a partir de la capacidad de un conductor esférico o de un condensador esférico con
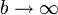
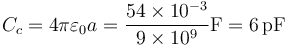
No hay más condensadores en el circuito equivalente. Aparte, habrá que colocar una resistencia entre los nodos 1 y 3, aunque en este primer apartado no es necesaria.





