Asociación de dos bombillas en serie

De Laplace

Revisión a fecha de 09:15 12 jun 2014; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

1 Enunciado

Se colocan en serie dos bombillas de potencias nominales 10 W y 6 W y se conectan a la red. Si la potencia radiada es proporcional a la potencia consumida, ¿cuál de las dos bombillas darán más luz? ¿En qué proporción?

2 Solución

La tentación, ante este problema, es hacer una de estas afirmaciones:

Emite más luz la de 10W (un 66% más sobre la de 6W).
Al estar en serie, ambas bombillas emiten la misma luz.

Ambas afirmaciones son incorrectas.

En serie, emite más luz la de 6W que la de 10W, como puede comprobarse de manera experimental sencilla.

La razón es la siguiente: Al estar en serie, por las dos bombillas circula la misma corriente, y la potencia que consume cada una es

No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): P_1 = I^2 R_1\qquad\qquadP_2 = I^2 R_2\,

o, en términos relativos

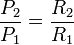
$\frac{P_2}{P_1}=\frac{R_2}{R_1}$

Así que la cuestión se reduce a ¿cuál de las de las dos bombillas tiene mayor resistencia? Y la respuesta es: la de menor potencia nominal.

La razón es que la potencia nominal se refiere a la que consume cuando se conecta a una tensión fijada (220V, habitualmente), por lo que

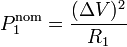
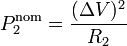
$P_1^\mathrm{nom} = \frac{(\Delta V)^2}{R_1}\,$ $P_2^\mathrm{nom} = \frac{(\Delta V)^2}{R_2}\,$

Por tanto, cuanto mayor sea la potencia nominal, menor será la resistencia. En términos relativos

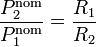
$\frac{P_2^\mathrm{nom}}{P_1^\mathrm{nom}}=\frac{R_1}{R_2}$

A partir del dato del voltaje y la potencia nominal (que es con lo que se suelen etiquetar la bombillas, por ejemplo “220V 6W”) podemos hallar las resistencias

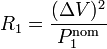
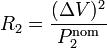
$R_1 = \frac{(\Delta V)^2}{P_1^\mathrm{nom}}$ $R_2 = \frac{(\Delta V)^2}{P_2^\mathrm{nom}}$

Sustituyendo en la potencia real tenemos

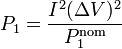
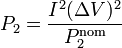
$P_1 = \frac{I^2(\Delta V)^2}{P_1^\mathrm{nom}}$ $P_2 = \frac{I^2(\Delta V)^2}{P_2^\mathrm{nom}}$

esto es, para las dos bombillas en serie, mayor potencia nominal implica menor potencia real. La relación entre las potencias reales es

$\frac{P_1}{P_2}=\frac{P_2^\mathrm{nom}}{P_1^\mathrm{nom}}$

así que la bombilla de 6W nominales emitirá un 66% más de luz que la de 10W.

Podemos hallar la potencia real de cada una, ya que la corriente que circula por ellas es la tensión total dividida por la resistencia total

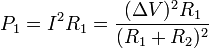
$P_1 = I^2 R_1 = \frac{(\Delta V)^2 R_1}{(R_1+R_2)^2}$

Sustituyendo la resistencia en función de la potencia nominal queda

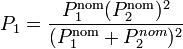
$P_1 = \frac{P_1^\mathrm{nom}(P_2^\mathrm{nom})^2}{(P_1^\mathrm{nom}+P_2^{nom})^2}$ $P_2 = \frac{(P_1^\mathrm{nom})^2P_2^\mathrm{nom}}{(P_1^\mathrm{nom}+P_2^{nom})^2}$

Si

$P_1^\mathrm{nom} = 10\,\mathrm{W}\qquad\qquad P_2^\mathrm{nom} = 6\,\mathrm{W}$

queda

$P_1 = 1.406\,\mathrm{W}\qquad\qquad P_2 = 2.344\,\mathrm{W}$

Vemos que además, ambas consumen muy por debajo de su valor nominal.

Asociación de dos bombillas en serie

De Laplace

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES