Preguntas de test de electrostática en el vacío (GIE)
De Laplace
- A Se tienen cuatro cargas en los vértices consecutivos de un cuadrado
ABCD de lado  , siendo sus valores
, siendo sus valores 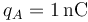 ,
, 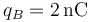 ,
,
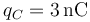 ,
, 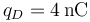 . ¿Cuánto vale
el flujo del campo eléctrico multiplicado por
. ¿Cuánto vale
el flujo del campo eléctrico multiplicado por  a
través de una esfera centrada en la primera carga y de radio 12\,cm?
a
través de una esfera centrada en la primera carga y de radio 12\,cm?
- A 6\,nC :*A 1\,nC :*A 10\,nC :*A 7\,nC
6 =
Se tienen cuatro cargas en los vértices de un cuadrado cuya diagonal mide
20\,cm, según ilustra la figura. Los valores de todas las cargas son +10\,nC o
− 10\,nC y 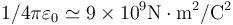
- A ¿Cuánto vale aproximadamente la fuerza sobre una carga de 10\,nC
situada en el centro del cuadrado?
- A
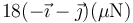 :*A
:*A
- A
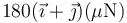 :*A Es nula
:*A Es nula
- A
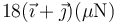
- A
\end{minipage} \begin{minipage}[t]{0.5\textwidth}
\begin{center} \includegraphics{4cargas-cuadrado.eps} \end{center} \end{minipage}
- A ¿Cuánto vale aproximadamente el trabajo para llevar la carga central
hasta el infinito?
- A No hay información suficiente para hallarlo. :*A
− 36\,μJ. :*A +36\,μJ.
- A Es nulo.
- A Suponiendo que no está la carga central, ¿cuánto vale la energía
electrostática almacenada en el sistema?
- A Es nula. :*A − 9\,μJ. :*A
+9\,μJ. :*A No hay información suficiente para hallarla.
\newpage
6 =
Se tiene únicamente una distribución uniforme de una carga Q < 0 sobre una superficie esférica de radio a. Para los tres puntos de la figura,
- A ¿En cuál es mayor en módulo el campo eléctrico?
- A En M. :*A En O. :*A No hay información suficiente para
saberlo. :*A En P.
\end{minipage} \begin{minipage}[t]{0.5\textwidth}
\begin{center} \includegraphics{esfera-tres-puntos.eps} \end{center} \end{minipage}
- A ¿Cómo se ordena el potencial de los tres puntos?
- A VO > VM < VP. :*A VO = VM > VP.
- A VO < VM > VP.
- A VO = VM < VP.
- A Dos cargas puntuales positivas q1 y q2 se
encuentran a una distancia a. Si la distancia entre ellas se reduce a la mitad, ¿cómo cambia la energía electrostática del sistema?
- A Aumenta al cuádruple :*A Se reduce a la mitad. :*A
Aumenta al doble. :*A No cambia.
- A En los dos extremos de una barra rígida se encuentran cargas de la
misma magnitud y signo opuesto. La barra se encuentra inicialmente en reposo y sumergida en un campo eléctrico uniforme, formando un cierto ángulo con el campo. ¿Qué efecto produce el campo sobre la barra?
- A Ninguno. Las fuerzas se cancelan y la barra permanece en reposo.
- A Produce un par de fuerzas que tiende a alinear la barra con el campo.
- A Produce un par de fuerzas que tiende a colocar la barra perpendicular
al campo. :*A Produce una fuerza neta que tiende a desplazar la barra.
% 8
\newpage
Se tiene una distribución de carga formada por una esfera de radio b cargada uniformemente con una densidad volumétrica de carga ρ0, Esta esfera está forrada por una superficie esférica (también de radio b) con densidad de carga superficial σ0, de tal forma que la carga total del sistema es nula.
- A ¿Cuánto vale σ0?
- A − ρ0b :*A − ρ0 :*A
− 4πb2ρ0 :*A − ρ0b / 3
- A Para esta distribución de carga, ¿cuánto vale el campo eléctrico que
produce?
- A Es nulo en el interior de la esfera y vale
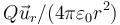 en el exterior con
Q = (4πb3 / 3)ρ0. :*A Es nulo en el interior de la
esfera y vale
en el exterior con
Q = (4πb3 / 3)ρ0. :*A Es nulo en el interior de la
esfera y vale 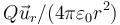 en el exterior
con Q = (4πb2)σ0. :*A Es nulo en todos los puntos
del espacio. :*A Es nulo en el exterior de la esfera y vale
en el exterior
con Q = (4πb2)σ0. :*A Es nulo en todos los puntos
del espacio. :*A Es nulo en el exterior de la esfera y vale 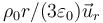 en el interior.
en el interior.
- A Para este sistema, ¿cuánto vale el potencial eléctrico en el centro
de la esfera?
- A
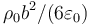 , :*A Es nulo.
, :*A Es nulo.
- A Tiende a infinito. :*A
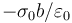 .
.
- A
Una carga puntual de valor 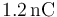 se encuentra situada
en el punto
se encuentra situada
en el punto 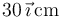 y una de valor
y una de valor
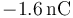 en
en 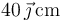 .
Dato:
.
Dato: 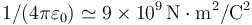
- A ¿Cuánto vale, en módulo, el campo en
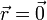 ?
?
- A ¿Cuánto vale, en módulo, el campo en
- A 30\,V/m :*A 150\,V/m :*A 210\,V/m :*A
− 30\,V/m
- A ¿Y el potencial eléctrico en el mismo punto
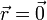 ?
?
- A
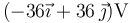 :*A
:*A
- A
72\,V. :*A 210\,V. :*A 0\,V.
%
- A Un franklin es una unidad de carga eléctrica definida como aquella
tal que dos cargas de 1 franklin situadas a 1\,cm se ejercen una fuerza de 1\,dina ( = 10 − 5N). ¿A cuantos culombios equivale un franklin?
- A
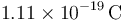 :*A
:*A
- A
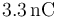 :*A
:*A 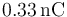
- A
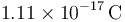
- A
6
- A Dada una cierta distribución de potencial eléctrico, el campo
eléctrico apunta en el sentido\ldots
- A en que decrece el potencial. :*A tangente a las superficies
equipotenciales. :*A en que crece o decrece el potencial, dependiendo de donde estén las cargas eléctricas. :*A en que crece el potencial.
6
- A Se tienen dos superficies esféricas concéntricas de radios
a y 2a, centradas en el origen de coordenadas. La
interior está cargada con una densidad superficial uniforme
+ σ0 y la exterior con una − σ0. El campo
eléctrico en un punto a 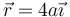 vale
vale
- A
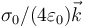 :*A
:*A
- A
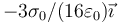 :*A
:*A
 :*A
:*A
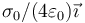
- A Para este sistema el potencial en el origen de coordenadas vale\ldots
- A
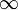 :*A 0 :*A
:*A 0 :*A
- A
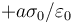 :*A
:*A
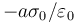
6
- A Una carga puntual se mueve en el seno de un campo eléctrico
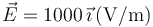 y de un campo
magnético
y de un campo
magnético 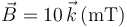 . ¿Con qué velocidad
debe moverse la carga para que la fuerza electromagnética sobre ella sea nula?
. ¿Con qué velocidad
debe moverse la carga para que la fuerza electromagnética sobre ella sea nula?
- A
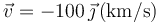
- A Es imposible que se anule la fuerza. :*A
- A
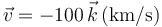 :*A
:*A