Energía electrostática de un sistema de conductores (F2 GIA)
De Laplace
1 Descripción del sistema
Sea un sistema formado por N conductores ideales,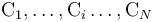 , con carga eléctrica distribuidas en sus superficies:
, con carga eléctrica distribuidas en sus superficies:
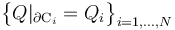
Dicha distribución de carga generá un campo eléctrico y, por consiguiente, un campo escalar de potencial electrostático 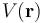 . Como se sabe, si el sistema se encuentra en equilibrio electrostático, todos los puntos de cada conductor se hallan al mismo potencial y, por tanto, las superficies condctoras son equipotenciales; es decir, dicho campo escalar va a ser tal que en los puntos de cada superficie
. Como se sabe, si el sistema se encuentra en equilibrio electrostático, todos los puntos de cada conductor se hallan al mismo potencial y, por tanto, las superficies condctoras son equipotenciales; es decir, dicho campo escalar va a ser tal que en los puntos de cada superficie 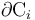 tendrá el mismo valor Vi, medido respecto de cualquier otro conductor que se halle conectado “a tierra” (conductor C0) y que, por tanto, consideramos a potencial cero:
tendrá el mismo valor Vi, medido respecto de cualquier otro conductor que se halle conectado “a tierra” (conductor C0) y que, por tanto, consideramos a potencial cero:

2 Cálculo de la energía electrostática almacenada en el sistema
En un sistema electrostático donde la carga eléctrica se distribuye de forma continua en una determinada región de fuentes 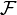 , la energía electrostática almacenada en el sistema responde a la expresión,
, la energía electrostática almacenada en el sistema responde a la expresión,
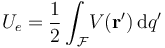
donde 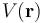 es el potencial electrostático creado por la distribución. Como se recordará, esta energía es el trabajo externo que ha sido necesario realizar para, mediante una serie de procesos cuasi--estáticos, configurar dicha distribución de carga eléctrica estática.
es el potencial electrostático creado por la distribución. Como se recordará, esta energía es el trabajo externo que ha sido necesario realizar para, mediante una serie de procesos cuasi--estáticos, configurar dicha distribución de carga eléctrica estática.
La región 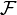 no ha de ser necesariamente conexa; es decir, puede estar formada por diferentes regiones, conectadas o no. En el caso del sistema bajo estudio, formado por conductores cargados, dicha región de fuentes está constituida por las superficies de los N conductores. En consecuencia, integral extendida a la región
no ha de ser necesariamente conexa; es decir, puede estar formada por diferentes regiones, conectadas o no. En el caso del sistema bajo estudio, formado por conductores cargados, dicha región de fuentes está constituida por las superficies de los N conductores. En consecuencia, integral extendida a la región 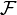 es equivalente a la suma de las N integrales correspondientes a las distintas superficies conductoras:
es equivalente a la suma de las N integrales correspondientes a las distintas superficies conductoras:
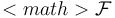 =\particl\mathrm{C}_1\bigcup\ldots\bigcup\partial\mathrm{C}_N\quad\Longrightarrow\quad U_e=\frac{1}{2}\ \sum_{i=1}^N\int_{\partial C_i}\! V(\mathbf{r}^\prime)\!\ \mathrm{d}q^\prime</math>
=\particl\mathrm{C}_1\bigcup\ldots\bigcup\partial\mathrm{C}_N\quad\Longrightarrow\quad U_e=\frac{1}{2}\ \sum_{i=1}^N\int_{\partial C_i}\! V(\mathbf{r}^\prime)\!\ \mathrm{d}q^\prime</math>
ba
Si las esferas conductoras del sistema analizado se cargan con sendas cantidades Q1 y Q2 de carga eléctrica, por ejemplo conectándolas a generadores que establezcan valores constantes del potencial en todos sus puntos, dichas cargas se distribuirán en el equilibrio exclusivamente en sus superficies 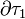 y
y 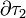 , según determinadas densidades superficiales,
, según determinadas densidades superficiales, 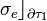 y
y 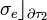 :
:
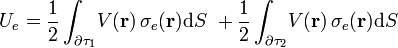
Por otra parte, cada una de las superficies conductoras es una superficie equipotencial en la que el potencial electrostático tiene idéntico valor en todos sus puntos. Por tanto, se tendrá:
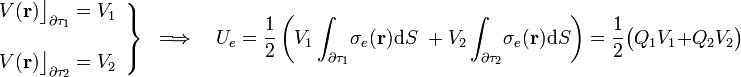
Por tanto, para calcular las cantidades de energía electrostática requeridos en el ejercicio, basta con determinar los valores de las cargas y los potenciales de las esferas conductoras en las dos situaciones indicadas.






