No Boletín - Cuestión sobre tres velocidades (Ex.Feb/14)

De Laplace

Revisión a fecha de 12:26 21 mar 2014; Enrique (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

1 Enunciado

Las posiciones y velocidades instantáneas de tres puntos de un sólido rígido vienen dadas por:

Punto	$\vec{r}$ (m)	$\vec{v}$ (m/s)
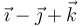
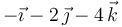
A	$\vec{\imath}-\vec{\jmath}+\vec{k}$	$-\vec{\imath}-2\,\vec{\jmath}-4\,\vec{k}$
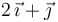
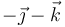
B	$2\,\vec{\imath}+\vec{\jmath}$	$-\vec{\jmath}-\vec{k}$
C	$\vec{0}$	$-\vec{\imath}+\vec{\jmath}-\vec{k}$

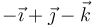
¿Cuál de las siguientes afirmaciones es verdadera?

(a) Estos datos son incompatibles con la rigidez

(b) La velocidad de deslizamiento (segundo invariante) vale 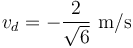$v_d=-\displaystyle\frac{2}{\sqrt{6}}\,\,\mathrm{m/s}\,$

(c) La velocidad angular (primer invariante) vale 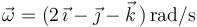$\vec{\omega}=(2\,\vec{\imath}-\vec{\jmath}-\vec{k}\,)\,\mathrm{rad/s}\,$

(d) El eje instantáneo de rotación pasa por el punto de coordenadas 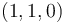$(1,1,0)\,$

2 Equiproyectividad. Descartando (a)

La condición cinemática de rigidez consiste en la equiproyectividad del campo de velocidades:

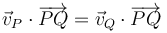
$\vec{v}_P\cdot\overrightarrow{PQ}=\vec{v}_Q\cdot\overrightarrow{PQ}$

Sometiendo a examen a cada par de puntos:

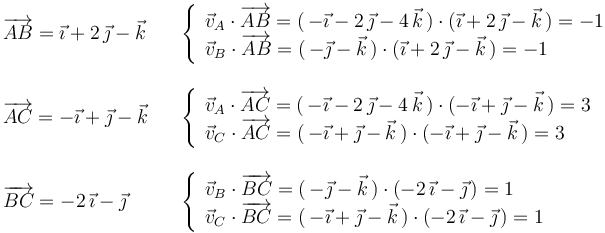
$\begin{array}{ll}\overrightarrow{AB}=\vec{\imath}+2\,\vec{\jmath}-\vec{k} & \,\,\,\,\,\left\{\begin{array}{l} \vec{v}_A\cdot\overrightarrow{AB}=(\,-\vec{\imath}-2\,\vec{\jmath}-4\,\vec{k}\,)\cdot(\vec{\imath}+2\,\vec{\jmath}-\vec{k}\,)=-1 \\ \vec{v}_B\cdot\overrightarrow{AB}=(\,-\vec{\jmath}-\vec{k}\,)\cdot(\vec{\imath}+2\,\vec{\jmath}-\vec{k}\,)=-1\end{array}\right. \\ \\ \overrightarrow{AC}=-\vec{\imath}+\vec{\jmath}-\vec{k} & \,\,\,\,\,\left\{\begin{array}{l} \vec{v}_A\cdot\overrightarrow{AC}=(\,-\vec{\imath}-2\,\vec{\jmath}-4\,\vec{k}\,)\cdot(-\vec{\imath}+\vec{\jmath}-\vec{k}\,)=3 \\ \vec{v}_C\cdot\overrightarrow{AC}=(\,-\vec{\imath}+\vec{\jmath}-\vec{k}\,)\cdot(-\vec{\imath}+\vec{\jmath}-\vec{k}\,)=3\end{array}\right. \\ \\ \overrightarrow{BC}=-2\,\vec{\imath}-\vec{\jmath} & \,\,\,\,\,\left\{\begin{array}{l} \vec{v}_B\cdot\overrightarrow{BC}=(\,-\vec{\jmath}-\vec{k}\,)\cdot(-2\,\vec{\imath}-\vec{\jmath}\,)=1 \\ \vec{v}_C\cdot\overrightarrow{BC}=(\,-\vec{\imath}+\vec{\jmath}-\vec{k}\,)\cdot(-2\,\vec{\imath}-\vec{\jmath}\,)=1\end{array}\right.\end{array}$

comprobamos que los datos del enunciado son compatibles con la rigidez, y por tanto la afirmación (a) es FALSA.

3 Cálculo de la velocidad angular. Descartando (c)

Podemos deducir el vector velocidad angular 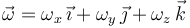$\,\vec{\omega}=\omega_x\,\vec{\imath}+\omega_y\,\vec{\jmath}+\omega_z\,\vec{k}\,\,$ del sólido, componente a componente, exigiendo el cumplimiento de la ecuación del campo de velocidades en la relación entre las velocidades conocidas.

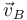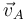Por ejemplo, la relación entre $\vec{v}_B\,$ y $\vec{v}_A\,$ debe satisfacer la ecuación:

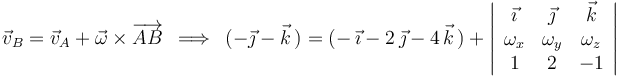
$\vec{v}_B=\vec{v}_A+\vec{\omega}\times\overrightarrow{AB}\,\,\,\Longrightarrow\,\,\,(-\vec{\jmath}-\vec{k}\,)=(-\,\vec{\imath}-2\,\vec{\jmath}-4\,\vec{k}\,)+\left|\begin{array}{ccc} \vec{\imath} & \vec{\jmath} & \vec{k} \\ \omega_x & \omega_y & \omega_z \\ 1 & 2 & -1 \end{array}\right|$

E igualando componentes homólogas:

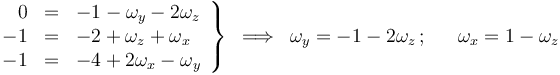
$\left.\begin{array}{rcl} 0 & = & -1-\omega_y-2\omega_z \\ -1 & = & -2+\omega_z+\omega_x \\ -1 & = & -4+2\omega_x-\omega_y \end{array}\right\}\,\,\,\Longrightarrow\,\,\, \omega_y=-1-2\omega_z\,;\,\,\,\,\,\,\,\,\,\omega_x=1-\omega_z$

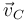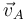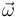Y relacionando de forma análoga $\vec{v}_C\,$ y $\vec{v}_A\,$ , podemos culminar la deducción de $\vec{\omega}\,$ :

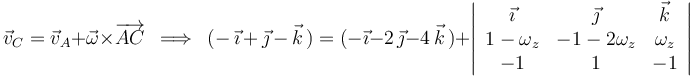
$\vec{v}_C=\vec{v}_A+\vec{\omega}\times\overrightarrow{AC}\,\,\,\Longrightarrow\,\,\,(-\,\vec{\imath}\,+\,\vec{\jmath}\,-\,\vec{k}\,)=(-\vec{\imath}-2\,\vec{\jmath}-4\,\vec{k}\,)+\left|\begin{array}{ccc} \vec{\imath} & \vec{\jmath} & \vec{k} \\ 1-\omega_z & -1-2\omega_z & \omega_z \\ -1 & 1 & -1 \end{array}\right|$

E igualando componentes homólogas:

$\left.\begin{array}{rcl} -1 & = & -1+2\omega_z+1-\omega_z \\ 1 & = & -2-\omega_z+1-\omega_z \\ -1 & = & -4+1-\omega_z-2\omega_z-1 \end{array}\right\}\,\,\,\Longrightarrow\,\,\, \omega_z=-1\,;\,\,\,\,\,\,\,\,\,\omega_y=1\,;\,\,\,\,\,\,\,\,\,\omega_x=2$

Por tanto, el vector velocidad angular (primer invariante) es:

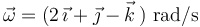
$\vec{\omega}=(2\,\vec{\imath}+\vec{\jmath}-\vec{k}\,)\,\,\mathrm{rad/s}$

Puede observarse que el valor obtenido de 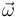$\vec{\omega}\,$ no coincide con el propuesto en la afirmación (c). En concreto, la discrepancia está en el signo de la segunda componente. Por tanto, la afirmación (c) es FALSA.

No Boletín - Cuestión sobre tres velocidades (Ex.Feb/14)

De Laplace

1 Enunciado

2 Equiproyectividad. Descartando (a)

3 Cálculo de la velocidad angular. Descartando (c)

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES