No Boletín - Cuestión sobre tres velocidades (Ex.Feb/14)

De Laplace

Revisión a fecha de 11:47 21 mar 2014; Enrique (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

1 Enunciado

Las posiciones y velocidades instantáneas de tres puntos de un sólido rígido vienen dadas por:

Punto	$\vec{r}$ (m)	$\vec{v}$ (m/s)
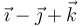
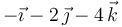
A	$\vec{\imath}-\vec{\jmath}+\vec{k}$	$-\vec{\imath}-2\,\vec{\jmath}-4\,\vec{k}$
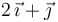
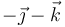
B	$2\,\vec{\imath}+\vec{\jmath}$	$-\vec{\jmath}-\vec{k}$
C	$\vec{0}$	$-\vec{\imath}+\vec{\jmath}-\vec{k}$

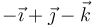
¿Cuál de las siguientes afirmaciones es verdadera?

(a) Estos datos son incompatibles con la rigidez

(b) La velocidad de deslizamiento (segundo invariante) vale 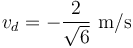$v_d=-\displaystyle\frac{2}{\sqrt{6}}\,\,\mathrm{m/s}\,$

(c) La velocidad angular (primer invariante) vale 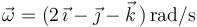$\vec{\omega}=(2\,\vec{\imath}-\vec{\jmath}-\vec{k}\,)\,\mathrm{rad/s}\,$

(d) El eje instantáneo de rotación pasa por el punto de coordenadas 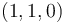$(1,1,0)\,$

2 Equiproyectividad. Descartando (a)

La condición cinemática de rigidez consiste en la equiproyectividad del campo de velocidades:

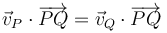
$\vec{v}_P\cdot\overrightarrow{PQ}=\vec{v}_Q\cdot\overrightarrow{PQ}$

Sometiendo a examen a cada par de puntos:

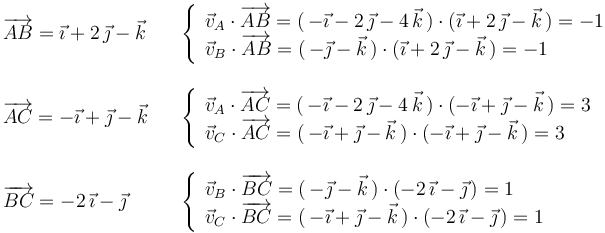
$\begin{array}{ll}\overrightarrow{AB}=\vec{\imath}+2\,\vec{\jmath}-\vec{k} & \,\,\,\,\,\left\{\begin{array}{l} \vec{v}_A\cdot\overrightarrow{AB}=(\,-\vec{\imath}-2\,\vec{\jmath}-4\,\vec{k}\,)\cdot(\vec{\imath}+2\,\vec{\jmath}-\vec{k}\,)=-1 \\ \vec{v}_B\cdot\overrightarrow{AB}=(\,-\vec{\jmath}-\vec{k}\,)\cdot(\vec{\imath}+2\,\vec{\jmath}-\vec{k}\,)=-1\end{array}\right. \\ \\ \overrightarrow{AC}=-\vec{\imath}+\vec{\jmath}-\vec{k} & \,\,\,\,\,\left\{\begin{array}{l} \vec{v}_A\cdot\overrightarrow{AC}=(\,-\vec{\imath}-2\,\vec{\jmath}-4\,\vec{k}\,)\cdot(-\vec{\imath}+\vec{\jmath}-\vec{k}\,)=3 \\ \vec{v}_C\cdot\overrightarrow{AC}=(\,-\vec{\imath}+\vec{\jmath}-\vec{k}\,)\cdot(-\vec{\imath}+\vec{\jmath}-\vec{k}\,)=3\end{array}\right. \\ \\ \overrightarrow{BC}=-2\,\vec{\imath}-\vec{\jmath} & \,\,\,\,\,\left\{\begin{array}{l} \vec{v}_B\cdot\overrightarrow{BC}=(\,-\vec{\jmath}-\vec{k}\,)\cdot(-2\,\vec{\imath}-\vec{\jmath}\,)=1 \\ \vec{v}_C\cdot\overrightarrow{BC}=(\,-\vec{\imath}+\vec{\jmath}-\vec{k}\,)\cdot(-2\,\vec{\imath}-\vec{\jmath}\,)=1\end{array}\right.\end{array}$

comprobamos que los datos del enunciado son compatibles con la rigidez, y por tanto la afirmación (a) es FALSA.

No Boletín - Cuestión sobre tres velocidades (Ex.Feb/14)

De Laplace

1 Enunciado

2 Equiproyectividad. Descartando (a)

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES