No Boletín - Identificación de movimiento III (Ex.Oct/13)

De Laplace

Revisión a fecha de 11:38 20 mar 2014; Enrique (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

1 Enunciado

En el triedro cartesiano 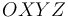$OXYZ\,$ , una partícula $P\,$ se mueve conforme a la ecuación horaria:

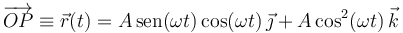
$\overrightarrow{OP}\equiv\vec{r}(t)=A\,\mathrm{sen}(\omega t)\,\mathrm{cos}(\omega t) \,\vec{\jmath}+A\,\mathrm{cos}^2(\omega t)\,\vec{k}$

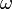donde $A\,$ y $\omega\,$ son constantes conocidas.

¿Qué trayectoria sigue la partícula?
¿Con qué tipo de movimiento es recorrida dicha trayectoria?

2 Solución

Esta cuestión se resuelve rápidamente si se utilizan las relaciones trigonométricas:

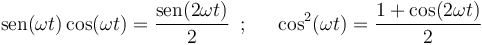
$\mathrm{sen}(\omega t)\,\mathrm{cos}(\omega t)=\frac{\mathrm{sen}(2\omega t)}{2}\,\,\,;\,\,\,\,\,\,\,\,\, \mathrm{cos}^2(\omega t)=\frac{1+\mathrm{cos}(2\omega t)}{2}$

que permiten reescribir la ecuación horaria de la partícula $P\,$ como:

$\overrightarrow{OP}\equiv\vec{r}(t)=\frac{A}{2}\,\vec{k}+\left[\frac{A}{2}\,\mathrm{sen}(2\omega t)\,\vec{\jmath}+\frac{A}{2}\,\mathrm{cos}(2\omega t)\,\vec{k}\,\right]$

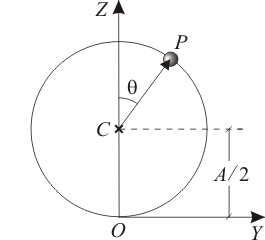
Así escrita, la ecuación horaria es fácilmente reconocible como la del movimiento sobre una circunferencia contenida en el plano 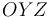$OYZ\,$ , con centro en el punto $C(0,0,A/2)\,$ , con radio 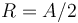$R=A/2\,$ , y con ecuación vectorial $\theta\,$ -paramétrica:

$\overrightarrow{OP}\equiv\vec{r}(\theta)=\frac{A}{2}\,\vec{k}+\left[\frac{A}{2}\,\mathrm{sen}(\theta)\,\vec{\jmath}+\frac{A}{2}\,\mathrm{cos}(\theta)\,\vec{k}\,\right]$

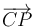donde $\theta\,$ es el ángulo formado por el vector $\overrightarrow{CP}\,$ y el eje $OZ\,$ (ver figura), y varía conforme a la ley horaria:

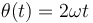
$\theta(t)=2\omega t\,$

La trayectoria es, por tanto, una circunferencia; y el tipo de movimiento con que se recorre ésta es un movimiento uniforme, ya que la celeridad $v\,$ de la partícula es constante en el tiempo:

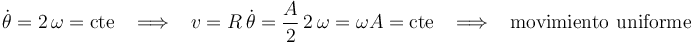
$\dot{\theta}=2\,\omega=\mathrm{cte}\,\,\,\,\,\Longrightarrow\,\,\,\,\, v=R\,\dot{\theta}=\frac{A}{2}\,2\,\omega=\omega A=\mathrm{cte}\,\,\,\,\,\Longrightarrow\,\,\,\,\,\mathrm{movimiento}\,\,\mathrm{uniforme}$

3 Solución alternativa

Un procedimiento alternativo menos directo consiste en ir analizando las características geométricas y cinemáticas del movimiento propuesto hasta lograr responder las preguntas formuladas.

Derivando el vector de posición de la partícula respecto al tiempo, obtenemos el vector velocidad:

$\vec{v}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}=\omega A\left\{\left[\mathrm{cos}^2(\omega t)-\mathrm{sen}^2(\omega t)\,\right]\vec{\jmath}-2\,\mathrm{sen}(\omega t)\,\mathrm{cos}(\omega t)\,\vec{k}\,\right\}=\omega A\left[\mathrm{cos}(2\omega t)\,\vec{\jmath}-\mathrm{sen}(2\omega t)\,\vec{k}\,\right]$

Y tomando el módulo de la velocidad, calculamos la celeridad:

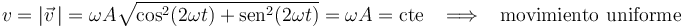
$v=|\vec{v}\,|=\omega A\sqrt{\mbox{cos}^2(2\omega t)+\mbox{sen}^2(2\omega t)}=\omega A=\mathrm{cte}\,\,\,\,\,\Longrightarrow\,\,\,\,\,\mathrm{movimiento}\,\,\mathrm{uniforme}$

Al ser la celeridad de la partícula constante, deducimos que se trata de un movimiento uniforme.

Derivando respecto al tiempo el vector velocidad, obtenemos el vector aceleración:

$\vec{a}=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}=-2\omega^2\! A\left[\mathrm{sen}(2\omega t)\,\vec{\jmath}+\mathrm{cos}(2\omega t)\,\vec{k}\,\right]$

Al tratarse de un movimiento uniforme, la aceleración tangencial es nula:

$a_t=\frac{\mathrm{d}v}{\mathrm{d}t}=\frac{\mathrm{d}(\omega A)}{\mathrm{d}t}=0$

y entonces la aceleración normal (siempre positiva) coincide con el módulo del vector aceleración:

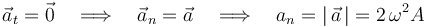
$\vec{a}_t=\vec{0}\,\,\,\,\,\,\Longrightarrow\,\,\,\,\,\,\vec{a}_n=\vec{a}\,\,\,\,\,\,\Longrightarrow\,\,\,\,\,\, a_n=|\,\vec{a}\,|=2\,\omega^2 A$

Obtenemos el vector tangente a la trayectoria como un vector unitario en la dirección de la velocidad:

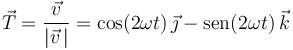
$\vec{T}=\frac{\vec{v}}{|\vec{v}\,|}=\mathrm{cos}(2\omega t)\,\vec{\jmath}-\mathrm{sen}(2\omega t)\,\vec{k}$

Dado que sabemos que toda la aceleración es normal (no existe componente tangencial), obtenemos el vector normal principal simplemente normalizando el vector aceleración:

$\vec{N}=\frac{\vec{a}_n}{a_n}=\frac{\vec{a}}{|\,\vec{a}\,|}=-\,\mathrm{sen}(2\omega t)\,\vec{\jmath}-\,\mathrm{cos}(2\omega t)\,\vec{k}$

Ahora hallamos el vector binormal como producto vectorial del vector tangente y el vector normal principal:

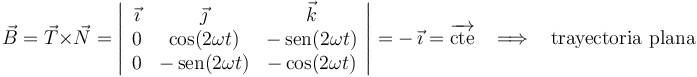
$\vec{B}=\vec{T}\times\vec{N} = \left|\begin{array}{ccc} \vec{\imath} & \vec{\jmath} & \vec{k} \\ 0 & \mathrm{cos}(2\omega t) & -\,\mathrm{sen}(2\omega t) \\ 0 & -\,\mathrm{sen}(2\omega t) & -\,\mathrm{cos}(2\omega t) \end{array}\right|=-\,\vec{\imath}=\overrightarrow{\mathrm{cte}}\,\,\,\,\,\Longrightarrow\,\,\,\,\,\mathrm{trayectoria}\,\,\mathrm{plana}$

Vemos que resulta un vector binormal constante, lo cual implica que la trayectoria de la partícula es plana.

Hallamos el radio de curvatura a partir de la celeridad y la aceleración normal:

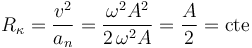
$R_{\kappa} = \frac{v^2}{a_n} = \frac{\omega^2 A^2}{2\,\omega^2 A}=\frac{A}{2}=\mathrm{cte}$

Observamos que el radio de curvatura resulta ser constante.

Dado que la trayectoria es plana y tiene radio de curvatura constante, llegamos a la conclusión de que se trata de una circunferencia.

Las dos preguntas del enunciado quedan, pues, respondidas si decimos que la partícula describe un movimiento circular uniforme.

No Boletín - Identificación de movimiento III (Ex.Oct/13)

De Laplace

1 Enunciado

2 Solución

3 Solución alternativa

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES