No Boletín - Identificación de movimiento III (Ex.Oct/13)

De Laplace

Revisión a fecha de 18:42 19 mar 2014; Enrique (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

1 Enunciado

En el triedro cartesiano 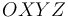$OXYZ\,$ , una partícula $P\,$ se mueve conforme a la ecuación horaria:

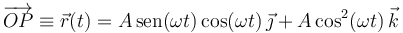
$\overrightarrow{OP}\equiv\vec{r}(t)=A\,\mathrm{sen}(\omega t)\,\mathrm{cos}(\omega t) \,\vec{\jmath}+A\,\mathrm{cos}^2(\omega t)\,\vec{k}$

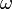donde $A\,$ y $\omega\,$ son constantes conocidas.

¿Qué trayectoria sigue la partícula?
¿Con qué tipo de movimiento es recorrida dicha trayectoria?

2 Solución

Esta cuestión se resuelve rápidamente si se utilizan las relaciones trigonométricas:

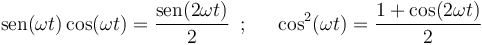
$\mathrm{sen}(\omega t)\,\mathrm{cos}(\omega t)=\frac{\mathrm{sen}(2\omega t)}{2}\,\,\,;\,\,\,\,\,\,\,\,\, \mathrm{cos}^2(\omega t)=\frac{1+\mathrm{cos}(2\omega t)}{2}$

que permiten reescribir la ecuación horaria de la partícula $P\,$ como:

$\overrightarrow{OP}\equiv\vec{r}(t)=\frac{A}{2}\,\vec{k}+\left[\frac{A}{2}\,\mathrm{sen}(2\omega t)\,\vec{\jmath}+\frac{A}{2}\,\mathrm{cos}(2\omega t)\,\vec{k}\,\right]$

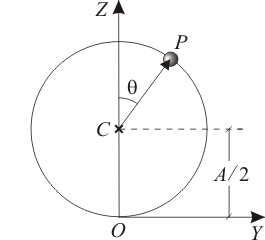
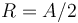Y esta ecuación horaria es reconocible como la que corresponde al movimiento sobre una circunferencia con centro en el punto $C(0,0,A/2)\,$ , de radio $R=A/2\,$ , y con ecuación vectorial $\theta\,$ -paramétrica:

$\overrightarrow{OP}\equiv\vec{r}(\theta)=\frac{A}{2}\,\vec{k}+\left[\frac{A}{2}\,\mathrm{sen}(\theta)\,\vec{\jmath}+\frac{A}{2}\,\mathrm{cos}(\theta)\,\vec{k}\,\right]$

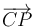donde $\theta\,$ es el ángulo formado por el vector $\overrightarrow{CP}\,$ y el eje $OZ\,$ (ver figura), y varía conforme a la ley horaria:

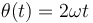
$\theta(t)=2\omega t\,$

La trayectoria es, por tanto, una circunferencia; y el tipo de movimiento con que se recorre ésta es un movimiento uniforme, ya que la celeridad de la partícula es constante en el tiempo:

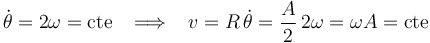
$\dot{\theta}=2\omega=\mathrm{cte}\,\,\,\,\,\Longrightarrow\,\,\,\,\, v=R\,\dot{\theta}=\frac{A}{2}\,2\omega=\omega A=\mathrm{cte}$

3 Solución alternativa

Un procedimiento alternativo menos directo consiste en ir analizando las características geométricas y cinemáticas del movimiento propuesto hasta lograr responder las preguntas formuladas.

Derivando el vector de posición de la partícula respecto al tiempo, obtenemos el vector velocidad:

$\vec{v}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}=\omega A\left\{\left[\mathrm{cos}^2(\omega t)-\mathrm{sen}^2(\omega t)\,\right]\,\vec{\jmath}-2\,\mathrm{sen}(\omega t)\,\mathrm{cos}(\omega t)\,\vec{k}\,\right\}=\omega A\left[\mathrm{cos}(2\omega t)\,\vec{\jmath}-\mathrm{sen}(2\omega t)\,\vec{k}\,\right]$

Y tomando módulo, calculamos la celeridad:

$v=|\vec{v}\,|=\omega A\sqrt{\mbox{cos}^2(2\omega t)+\mbox{sen}^2(2\omega t)}=\omega A=\mathrm{cte}$

Al ser la celeridad de la partícula constante, deducimos que se trata de un movimiento uniforme.

Derivando respecto al tiempo el vector velocidad, obtenemos el vector aceleración:

$\vec{a}=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}=-2\omega^2 A\left[\mathrm{sen}(2\omega t)\,\vec{\jmath}+\mathrm{cos}(2\omega t)\,\vec{k}\,\right]$

Al tratarse de un movimiento uniforme, la aceleración tangencial es nula:

$a_t=\frac{\mathrm{d}v}{\mathrm{d}t}=\frac{\mathrm{d}(\omega A)}{\mathrm{d}t}=0$

y entonces la aceleración normal (siempre positiva) coincide con el módulo del vector aceleración:

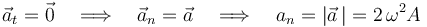
$\vec{a}_t=\vec{0}\,\,\,\,\,\,\Longrightarrow\,\,\,\,\,\,\vec{a}_n=\vec{a}\,\,\,\,\,\,\Longrightarrow\,\,\,\,\,\, a_n=|\vec{a}\,|=2\,\omega^2 A$

Obtenemos el vector tangente como un vector unitario en la dirección de la velocidad:

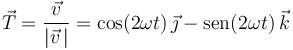
$\vec{T}=\frac{\vec{v}}{|\vec{v}\,|}=\mathrm{cos}(2\omega t)\,\vec{\jmath}-\mathrm{sen}(2\omega t)\,\vec{k}$

Dado que sabemos que toda la aceleración es normal (no existe componente tangencial), obtenemos el vector normal principal simplemente normalizando el vector aceleración:

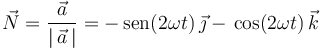
$\vec{N}=\frac{\vec{a}}{|\,\vec{a}\,|}=-\,\mathrm{sen}(2\omega t)\,\vec{\jmath}-\,\mathrm{cos}(2\omega t)\,\vec{k}$

Por último, hallamos el vector binormal como producto vectorial del vector tangente y el vector normal principal:

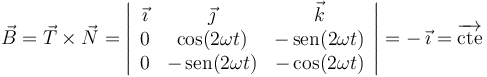
$\vec{B}=\vec{T}\times\vec{N} = \left|\begin{array}{ccc} \vec{\imath} & \vec{\jmath} & \vec{k} \\ 0 & \mathrm{cos}(2\omega t) & -\,\mathrm{sen}(2\omega t) \\ 0 & -\,\mathrm{sen}(2\omega t) & -\,\mathrm{cos}(2\omega t) \end{array}\right|=-\,\vec{\imath}=\overrightarrow{\mathrm{cte}}$

Vemos que resulta un vector binormal constante y, por tanto, podemos asegurar que la trayectoria es plana.

Nótese que otro procedimiento posible habría sido determinar primero el vector binormal normalizando el producto vectorial de velocidad por aceleración, y después calcular el vector normal como producto vectorial del binormal por el tangente.

Hallamos el radio de curvatura a partir de la celeridad y la aceleración normal:

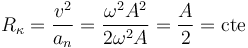
$R_{\kappa} = \frac{v^2}{a_n} = \frac{\omega^2 A^2}{2\omega^2 A}=\frac{A}{2}=\mathrm{cte}$

Obsérvese que el radio de curvatura resulta ser constante.

Puesto que la trayectoria es plana (vector binormal constante) y el radio de curvatura es constante, llegamos a la conclusión de que se trata de un movimiento circular.

Las dos preguntas del enunciado quedan, pues, respondidas si decimos que la partícula describe un movimiento circular uniforme.

No Boletín - Identificación de movimiento III (Ex.Oct/13)

De Laplace

1 Enunciado

2 Solución

3 Solución alternativa

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES