No Boletín - Identificación de movimiento III (Ex.Oct/13)
De Laplace
Revisión a fecha de 18:13 19 mar 2014; Enrique (Discusión | contribuciones)
1 Enunciado
En el triedro cartesiano 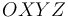 , una partícula
, una partícula  se mueve conforme a la ecuación horaria:
se mueve conforme a la ecuación horaria:
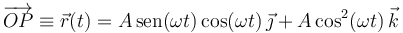
donde  y
y 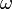 son constantes conocidas.
son constantes conocidas.
- ¿Qué trayectoria sigue la partícula?
- ¿Con qué tipo de movimiento es recorrida dicha trayectoria?
2 Solución
Esta cuestión se resuelve rápidamente si se utilizan las relaciones trigonométricas:
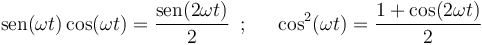
las cuales permiten reescribir la ecuación horaria de la partícula  como:
como:
![\overrightarrow{OP}\equiv\vec{r}(t)=\frac{A}{2}\,\vec{k}+\left[\frac{A}{2}\,\mathrm{sen}(2\omega t)\,\vec{\jmath}+\frac{A}{2}\,\mathrm{cos}(2\omega t)\,\vec{k}\right]](/wiki/images/math/4/e/b/4eb98153387d804e36acad04a5f1b69f.png)
Y esta ecuación horaria es reconocible como la que corresponde al movimiento sobre una circunferencia con centro en el punto  y radio
y radio 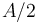 de ecuación vectorial
de ecuación vectorial  -paramétrica:
-paramétrica:
![\overrightarrow{OP}\equiv\vec{r}(\theta)=\frac{A}{2}\,\vec{k}+\left[\frac{A}{2}\,\mathrm{sen}(\theta)\,\vec{\jmath}+\frac{A}{2}\,\mathrm{cos}(\theta)\,\vec{k}\right]](/wiki/images/math/0/6/4/064dc47f5308077f211774e46c029e2b.png)
siendo  el ángulo formado por el vector de posición de la partícula
el ángulo formado por el vector de posición de la partícula 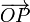 y el eje
y el eje  ), y que varía conforme a la ley horaria:
), y que varía conforme a la ley horaria:
la trayectoria es, por tanto, una circunferencia; y el tipo de movimiento con que se recorre la misma es un movimiento uniforme, ya que la celeridad es constante en el tiempo: