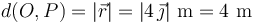No Boletín - Rectilíneo con aceleración creciente (Ex.Oct/13)
De Laplace
Revisión a fecha de 14:27 19 mar 2014; Enrique (Discusión | contribuciones)
1 Enunciado
Una partícula, inicialmente en reposo en el origen de coordenadas, se mueve con una aceleración creciente en el tiempo según la fórmula:
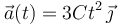
siendo  una constante de valor igual a
una constante de valor igual a 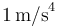 .
¿A qué distancia del origen de coordenadas se hallará la partícula en el instante
.
¿A qué distancia del origen de coordenadas se hallará la partícula en el instante 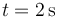 ?
?
2 Solución
Conforme a las definiciones de velocidad instantánea y aceleración instantánea, podemos escribir:
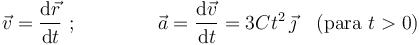
Conocemos también las condiciones iniciales de posición y velocidad:

Por tanto, determinar la velocidad y la posición de la partícula para 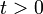 se reduce a integrar la aceleración una y dos veces, respectivamente, entre el instante inicial y un instante genérico:
se reduce a integrar la aceleración una y dos veces, respectivamente, entre el instante inicial y un instante genérico:

En el instante 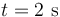 , la posición de la partícula es por tanto:
, la posición de la partícula es por tanto:
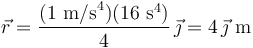
y su distancia al origen en dicho instante es: