No Boletín - Rectilíneo con aceleración creciente (Ex.Oct/13)

De Laplace

Revisión a fecha de 12:51 19 mar 2014; Enrique (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

1 Enunciado

Una partícula, inicialmente en reposo en el origen de coordenadas, se mueve con una aceleración creciente en el tiempo según la fórmula:

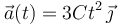
$\vec{a}(t)=3C t^2\,\vec{\jmath}$

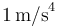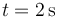siendo $C\,$ una constante de valor igual a $1\,\mathrm{m/s}^4\,$ . ¿A qué distancia del origen de coordenadas se hallará la partícula en el instante $t=2\,\mathrm{s}\,$ ?

2 Solución

Conforme a las definiciones de velocidad instantánea y aceleración instantánea, podemos escribir:

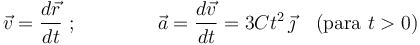
$\vec{v}=\frac{d\vec{r}}{dt}\,\, ;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \vec{a}=\frac{d\vec{v}}{dt}=3C t^2\,\vec{\jmath}\,\,\,\,\,\, (\mathrm{para}\,\, t>0)$

Conocemos también las condiciones iniciales de posición y velocidad:

$\vec{r}(0)=\vec{0}\,\mathrm{m}\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \vec{v}(0)=\vec{0}\,\mathrm{m/s}$

Por tanto, determinar la velocidad y la posición de la partícula para 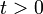$t>0\,$ se reduce a integrar la aceleración una y dos veces, respectivamente, entre el instante inicial y un instante genérico:

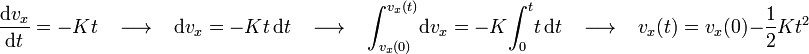
$\frac{\mathrm{d}v_x}{\mathrm{d}t}=-Kt\,\,\,\,\,\longrightarrow\,\,\,\,\,\mathrm{d}v_x=-Kt\,\mathrm{d}t\,\,\,\,\,\longrightarrow\,\,\,\,\,\int_{v_x(0)}^{v_x(t)}\!\mathrm{d}v_x=-K\!\int_{0}^{t}\!t\,\mathrm{d}t\,\,\,\,\,\longrightarrow\,\,\,\,\,v_x(t)=v_x(0)-\frac{1}{2}Kt^2$

$\frac{\mathrm{d}x}{\mathrm{d}t}=v_x(0)-\frac{1}{2}Kt^2\,\,\,\,\,\longrightarrow\,\,\,\,\,\mathrm{d}x=\left[v_x(0)-\frac{1}{2}Kt^2\right]\mathrm{d}t\,\,\,\,\,\longrightarrow\,\,\,\,\,\int_{x(0)}^{x(t)}\!\mathrm{d}x=\int_{0}^{t}\!\left[v_x(0)-\frac{1}{2}Kt^2\right]\mathrm{d}t\,\,\,\,\,\longrightarrow\,\,\,\,\,x(t)=x(0)+v_x(0)t-\frac{1}{6}Kt^3$

Observamos que se trata de un movimiento con velocidad inicial nula (inicialmente en reposo) y con una aceleración de módulo variable en el tiempo pero de dirección y sentido constantes. Es fácil comprender entonces que el movimiento es rectilíneo (ya que la velocidad Se trata de un movimiento rectilíneo a lo largo del eje OX. Por tanto, podemos escribir:

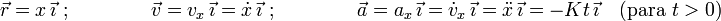
$\vec{r}=x\,\vec{\imath}\,\, ;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \vec{v}=v_x\,\vec{\imath}=\dot{x}\,\vec{\imath}\,\, ;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \vec{a}=a_x\,\vec{\imath}=\dot{v}_x\,\vec{\imath}=\ddot{x}\,\vec{\imath}=-Kt\,\vec{\imath}\,\,\,\,\,\, (\mathrm{para}\,\, t>0)$

Considerando por simplicidad que el origen de coordenadas coincide con la posición de la partícula en el instante en que se detecta el obstáculo 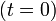$(t=0)\,$ , conocemos también las condiciones iniciales:

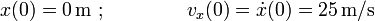
$x(0)=0\,\mathrm{m}\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, v_x(0)=\dot{x}(0)=25\,\mathrm{m}/\mathrm{s}$

Por tanto, determinar la velocidad y la posición de la partícula para 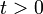$t>0\,$ se reduce a integrar la aceleración una y dos veces, respectivamente, entre el instante inicial y un instante genérico:

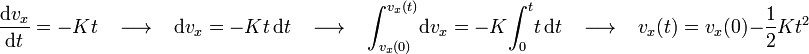
$\frac{\mathrm{d}v_x}{\mathrm{d}t}=-Kt\,\,\,\,\,\longrightarrow\,\,\,\,\,\mathrm{d}v_x=-Kt\,\mathrm{d}t\,\,\,\,\,\longrightarrow\,\,\,\,\,\int_{v_x(0)}^{v_x(t)}\!\mathrm{d}v_x=-K\!\int_{0}^{t}\!t\,\mathrm{d}t\,\,\,\,\,\longrightarrow\,\,\,\,\,v_x(t)=v_x(0)-\frac{1}{2}Kt^2$

$\frac{\mathrm{d}x}{\mathrm{d}t}=v_x(0)-\frac{1}{2}Kt^2\,\,\,\,\,\longrightarrow\,\,\,\,\,\mathrm{d}x=\left[v_x(0)-\frac{1}{2}Kt^2\right]\mathrm{d}t\,\,\,\,\,\longrightarrow\,\,\,\,\,\int_{x(0)}^{x(t)}\!\mathrm{d}x=\int_{0}^{t}\!\left[v_x(0)-\frac{1}{2}Kt^2\right]\mathrm{d}t\,\,\,\,\,\longrightarrow\,\,\,\,\,x(t)=x(0)+v_x(0)t-\frac{1}{6}Kt^3$

No Boletín - Rectilíneo con aceleración creciente (Ex.Oct/13)

De Laplace

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES