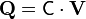Conductores esféricos concéntricos
De Laplace
Contenido |
1 Enunciado
Se tiene un sistema de dos conductores. Uno de ellos es una esfera metálica maciza de radio a. El otro es una fina corteza esférica metálica, de radio b, concéntrica con la anterior. Calcule el potencial en todos los puntos del espacio en los casos siguientes.- La esfera interior se encuentra a potencial V1 y la exterior a potencial V2.
- La esfera interior almacena una carga Q1 y la exterior una carga Q2.
- La esfera interior almacenada una carga Q1 y la exterior se encuentra a un potencial V2.
- Calcule asimismo la energía almacenada en el sistema de dos esferas, para las tres situaciones indicadas.
2 Solución
Este problema posee bastantes puntos en común con el de una sola esfera, en particular la simetría, por lo que se hará referencia a los resultados que allí se obtienen.
2.1 Caso de dos potenciales fijados
Cuando tenemos superficies conductoras cerradas, cuyos potenciales son conocidos, los problemas se desacoplan en varios independientes. Cada conductor funciona como una jaula de Faraday separando el problema interior del exterior.
En este caso, en que tenemos dos superficies esféricas concéntricas, el espacio se divide en tres regiones:
2.1.1 Región interior (r < a)
Tanto si se trata de una esfera maciza, como si es una superficie con una cavidad, el potencial en todos los puntos de la región interior es constante e igual a
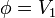
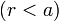
- Si se trata de un bloque macizo, porque el campo eléctrico en un material conductor en equilibrio electrostático es nulo y el potencial es, por tanto, uniforme.
- Si se trata de una superficie esférica con una cavidad, porque en el interior de dicha cavidad se verifica la ecuación de Laplace, con la condición de contorno de que en todos los puntos de la frontera el potencial es igual a V1, y la solución es igualmente la anterior.
2.1.2 Región intermedia (a < r < b)
En el hueco entre las dos esferas no hay carga intermedia, por lo que se verifica la ecuación de Laplace

con las condiciones de contorno
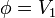

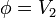
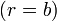
Por la simetría del sistema, podemos suponer que el potencial depende exclusivamente de la coordenada radial r. En este caso, la solución de la ecuación de Laplace es de la forma

Quedan por determinar las constantes A y B. Sustituyendo las condiciones de contorno
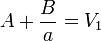
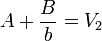
resultan las constantes y el potencial
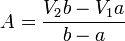
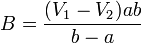
y sustituyendo las constantes en la expresión del potencial
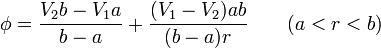
2.1.3 Región exterior (r > b)
Fuera de la esfera grande tenemos de nuevo simetría esférica, por lo que el potencial exterior es también de la forma
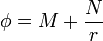
siendo en este caso las condiciones de contorno

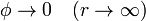
Este problema es exactamente el mismo que en el caso de una sola esfera, y por tanto su solución es idéntica
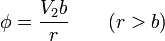
En términos físicos, lo que ocurre es que el conductor exterior actúa como una jaula de Faraday, haciendo que desde fuera se ignore por completo la existencia del conductor interior.
2.1.4 Potencial en todo el espacio
Reuniendo los tres resultados anteriores, nos queda la expreisón para el potencial
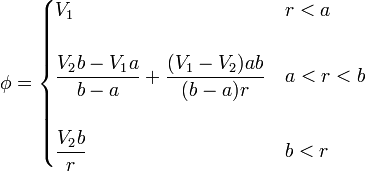
2.2 Caso de dos cargas conocidas
Si lo que conocemos son las cargas Q1 y Q2 de los dos conductores esféricas, la manera de operar que menos errores produce consiste en:
- Suponer ciertos potenciales V1 y V2,
- Aplicar (o resolver, si no se conoce) la solución del apartado anterior
- Hallar la relación entre las cargas y los voltajes en este sistema (a través de los coeficientes de capacidad).
- Calcular los voltajes en función de las cargas
- Sustituir los valores calculados en la expresión del potencial
En muchos casos existen atajos, si uno “ve” la solución, pero el procedimiento anterior es mucho más seguro.
2.2.1 Cálculo de las cargas
Suponemos entonces que la esfera interior se encuentra a un cierto potencial V1 y la corteza a un potencial V2, por lo que la expresión para el potencial es la que dimos anteriormente.
Se trata de hallar ahora la carga de cada conductor. La forma más sencilla en este caso consiste en identificar forma de la solución.
En la zona intermedia entre los conductores, el potencial es de la forma

que es el potencial debido a una carga puntual (más una constante, que no produce campo alguno). Identificando esta expresión con
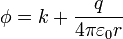
obtenemos la carga
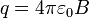
Esta carga es la interior a la distancia que estemos considerando. Puesto que estamos entre la esfera y la corteza, esta carga es la de la esfera maciza, esto es

Si ahora consideramos el exterior de la corteza esférica, el razonamiento es completamente análogo, salvo que ahora la carga interior es la contenida por ambos conductores
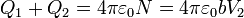
o, dicho de otra forma, desde fuerza detectamos una carga total Q1 + Q2, pero ignoramos cómo está distribuida en el interior.
Despejando de las dos relaciones anteriores, obtenemos los potenciales de las esferas en función de las cargas

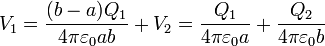
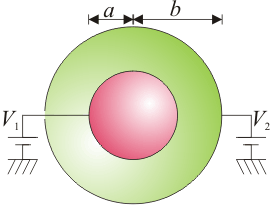
o, en forma matricial

Del mismo modo podemos hallar las cargas a partir de los potenciales

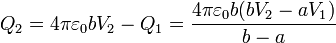
En forma matricial,