No Boletín - Detección de identidad falsa (Ex.Jun/13)
De Laplace
Contenido |
1 Enunciado
Sean tres sólidos rígidos ("0", "1" y "2") en movimiento relativo. ¿Cuál de las siguientes identidades es falsa?
1) 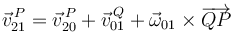
2) 
3) 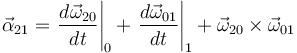
4) 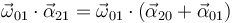
2 Identidad 1: Correcta
La identidad 1 se obtiene de sustituir la ecuación del campo de velocidades del movimiento {01} (aplicada a los puntos  y
y  ):
):
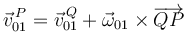
en la ley de composición de velocidades (aplicada en el punto  ):
):
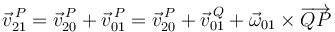
Por tanto, la identidad 1 es correcta.
3 Identidad 2: Correcta
La identidad 2 se obtiene de sustituir las definiciones de 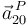 y
y 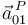 :
:
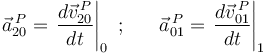
en la ley de composición de aceleraciones o teorema de Coriolis (aplicada en el punto  ):
):
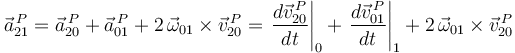
Por tanto, la identidad 2 es correcta.
4 Identidad 3: Falsa
Si se sustituyen las definiciones de 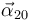 y
y 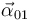 :
:
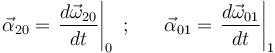
en la ley de composición de aceleraciones angulares:
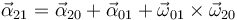
se obtiene la identidad:
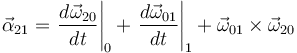
Pero observamos que la identidad 3 difiere de ésta en el último sumando, cuyo producto vectorial aparece permutado (lo cual equivale a un cambio de signo).
Por tanto, la identidad 3 es la falsa.
5 Identidad 4: Correcta
La identidad 4 se obtiene realizando el producto escalar de la ley de composición de aceleraciones angulares por el vector 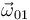 , operación que provoca la desaparición del último término debido a la ortogonalidad entre los vectores
, operación que provoca la desaparición del último término debido a la ortogonalidad entre los vectores 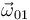 y
y  :
:
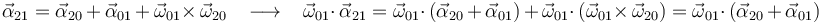
Por tanto, la identidad 4 es correcta.





