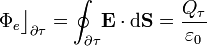Campo eléctrico de esfera cargada uniformemente FII GIA

De Laplace

Revisión a fecha de 18:11 10 mar 2014; Gabriel (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Solución

1 Enunciado

Una carga $Q$ se distribuye uniformemente en el volumen de una esfera de radio $R$ . Calcule el campo eléctrico dentro y fuera de la esfera.

2 Solución

2.1 Distribución de la carga

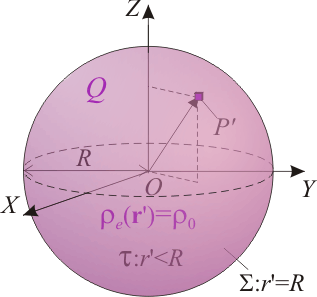
Consideramos una esfera

τ

de radio

R

con una cantidad

Q

de carga eléctrica distribuida uniformemente en todo su volumen. La distribución de carga estará descrita por la correspondiente densidad volumétrica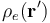 $\rho_e(\mathbf{r}')$ . La uniformidad de la distribución indica que en todos los puntos

P'

de la esfera

τ

superficie existirá la misma cantidad de carga por unidad de superficie, lo cuál es equivalente a que la relación entre la cantidad de carga contenida en un trozo arbitrario de esfera y el volumen de esta, debe ser constante. Si tomamos un sistema de referencia tal que su origen

O

coincida con el centro de la esfera, ésta vendrá descrita por la inecuación,

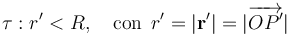
$\tau:r'<R\mathrm{,}\quad\,\mathrm{con}\,\;r'=|\mathbf{r}'|=|\overrightarrow{OP'}|$

...y la densidad volumétrica de carga...

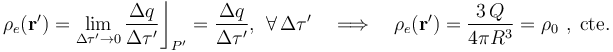
$\rho_e(\mathbf{r}')=\lim_{\Delta \tau'\rightarrow 0}\frac{\Delta q}{\Delta \tau'}\bigg\rfloor_{P'}=\frac{\Delta q}{\Delta \tau'}\mathrm{,}\;\;\forall\,\Delta \tau'\quad\Longrightarrow\quad\rho_e(\mathbf{r}')=\frac{3\!\ Q}{4\pi R^3}=\rho_0\ \mathrm{,}\;\,\mathrm{cte.}$

2.2 Simetría del campo eléctrico

La uniformidad y la geometría esférica de la distribución de carga nos lleva a formular la hipótesis de que el campo eléctrico que crea va a presentar un alto grado de simetría y, en consecuencia, puede ser fácilmente calculado mediante la Ley de Gauss.

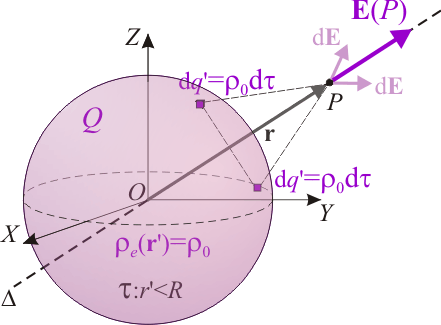
Para determinar esas propiedades de simetría consideraremos un punto $P$ arbitrario en el espacio y la recta $Δ$ que pasa por él y por el centro $O$ de la esfera. Obsérvese que para todo punto de la esfera cargada, existe otro simétricamente dispuesto respecto de dicha recta $Δ$ , encontrándose ambos a la misma distancia del punto $P$ donde queremos evaluar el campo eléctrico. Como la densidad volumétrica de carga es constante, en ambos habrá la misma cantidad infitesimal de carga, 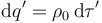$\mathrm{d}q^\prime=\rho_0\!\ \mathrm{d}\tau^\prime$ . En consecuencia, los diferenciales de campo eléctrico creados por dichas cargas suman sus componentes en la dirección del eje $Δ$ , pero se cancelan en la direcciones perpendiculares a dicho eje.

Y puesto que esto ocurre cualquiera que sea el par de puntos simétricos considerados en la esfera, la resultante del campo eléctrico en

P

, de toda la distribución de carga, va a ser colineal con la dirección

Δ

y, por tanto, con el segmento orientado $\overrightarrow{OP}$ . Por otra parte, como la elección de

P

es arbitraria, este resultado es extensible a todas las direcciones del espacio que pasen por el centro

O

de la esfera, obteniéndose además idéntico valor para la componente del campo en puntos que se hallen a igual distancia de

O

:

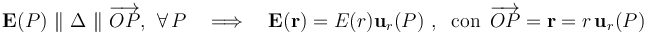
$\mathbf{E}(P)\ \|\ \Delta\ \|\ \overrightarrow{OP}\mathrm{,}\;\;\forall\, P\quad\Longrightarrow\quad\mathbf{E}(\mathbf{r})=E(r) \mathbf{u}_r(P)\ \mathrm{,}\;\ \,\mathrm{con}\,\;\overrightarrow{OP}=\mathbf{r}=r\!\ \mathbf{u}_r(P)$

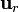siendo $\mathbf{u}_r$ el vector unitario en la dirección del radio-vector posición $\mathbf{r}$ . Se trataría, por tanto de un campo con simetría radial (como el de una carga puntual).

2.3 Aplicación de la Ley de Gauss

Establecida la dirección del campo eléctrico en cualquier punto del espacio, hemos de determinar ahora el valor de la componente $E (r)$ como una función de la distancia $r$ al centro de la esfera. Para ello procederemos a aplicar la ley del Gauss, según la cual el flujo del campo eléctrico a través de cualquier superficie cerrada $\partial \tau$ es proporcional a la cantidad de carga eléctrica encerrada en el interior de dicha superficie:

$\Phi_e\big\rfloor_{\partial\tau}=\oint_{\partial\tau}\!\mathbf{E}\cdot\mathrm{d}\mathbf{S}=\frac{Q_\tau}{\varepsilon_0}$

Campo eléctrico de esfera cargada uniformemente FII GIA

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Distribución de la carga

2.2 Simetría del campo eléctrico

2.3 Aplicación de la Ley de Gauss

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES