Trabajo en una compresión por un peso

De Laplace

Revisión a fecha de 19:56 21 feb 2014; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Introducción
3 Caso isotermo
4 Caso adiabático
5 Trabajo
- 5.1 Descenso con una pesa
- 5.2 Descenso acumulando arena
6 Energía interna
7 Calor

1 Enunciado

Un tubo vertical de sección cuadrada de 4.0 cm de lado contiene hidrógeno a 27°C y 100 kPa de presión, que también es la temperatura y presión exterior. La tapa del cilindro puede deslizarse sin rozamiento e inicialmente se encuentra a 10.0 cm de altura.

Suponiendo que las paredes del tubo son diatermas, calcule el trabajo realizado sobre el sistema entre el estado inicial y el estado de equilibrio final sí…
1. Se coloca bruscamente sobre la tapa una pesa de 4.0 kg.
2. Se colocan sobre el émbolo 4.0 kg de arena grano a grano.
Para los dos casos anteriores, halle la variación en la energía interna del gas y el calor que entra en el sistema durante el proceso.
Suponga ahora que las paredes del tubo son adiabáticas. ¿Cómo quedan en ese caso el trabajo, el calor y la variación de la energía interna para los dos procesos considerados?

2 Introducción

Este problema en realidad es una combinación de cuatro. En cada caso tenemos una compresión diferente:

Isoterma no cuasiestática
Isoterma cuasiestática
Adiabática no cuasiestática
Adiabática cuasiestática

En cada caso los resultados son diferentes, por lo que hay que tener claras las condiciones de cada proceso.

Cuando las paredes son diatermas, es decir, el tubo no está aislado térmicamente, la temperatura inicial y la final son iguales a la del ambiente, por lo que los procesos se pueden considerar isotermos.

Si las paredes son adiabáticas, no hay intercambio de calor entre el sistema y el entorno y la compresión es adiabática. En este caso, la temperatura final no tiene por qué coincidir con la del entorno.

Si la compresión se efectúa dejando caer una pesa sobre el émbolo, el proceso no es cuasiestático, ya que el gas experimenta un cambio brusco, pasando por estados no de equilibrio.

Si en cambio la masa se añade muy lentamente, puede suponerse que el proceso es cuasiestático y que el sistema está en todo momento en un estado de equilibrio.

3 Caso isotermo

Si las paredes no están aisladas térmicamente, el sistema es capaz de alcanzar el equilibrio térmico con el ambiente. Esto quiere decir que la temperatura inicial y la final son iguales a la del entorno

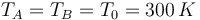
$T_A=T_B = T_0=300\,K$

Por otro lado, al ser un gas ideal, en un proceso a temperatura constante se cumple la ley de Boyle (caso particular de la de los gases ideales)

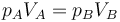
$p_AV_A = p_BV_B\,$

siendo la presión y el volumen iniciales

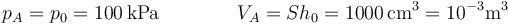
$p_A=p_0=100\,\mathrm{kPa}\qquad\qquad V_A = Sh_0 = 1000\,\mathrm{cm}^3 = 10^{-3}\mathrm{m}^3$

La presión final es la debida a la atmósfera más lo que aporta el peso. Tomando, por simplicidad $g = 10\,\mathrm{m}/\mathrm{s}^2$ queda

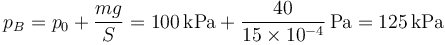
$p_B = p_0+\frac{mg}{S}=100\,\mathrm{kPa}+\frac{40}{15\times 10^{-4}}\,\mathrm{Pa}=125\,\mathrm{kPa}$

De aquí obtenemos el volumen final

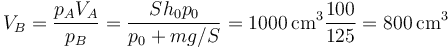
$V_B = \frac{p_AV_A}{p_B}=\frac{Sh_0p_0}{p_0+mg/S}=1000\,\mathrm{cm}^3\frac{100}{125}=800\,\mathrm{cm}^3$

siendo la nueva altura del pistón

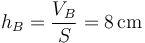
$h_B = \frac{V_B}{S}=8\,\mathrm{cm}$

4 Caso adiabático

5 Trabajo

Este problema es una continuación de uno anterior en el que hallaba la posición de equilibrio. Esta posición se halla mediante la ecuación de estado de los gases ideales

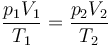
$\frac{p_1V_1}{T_1}=\frac{p_2V_2}{T_2}$

donde, al ser isotermo el proceso $T 1 = T 2$ , el volumen es la base por la altura, $V = S h$ y la presión inicial es la atmosférica, y la final es la atmosférica más la debida al peso

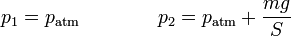
$p_1 = p_\mathrm{atm}\qquad\qquad p_2=p_\mathrm{atm}+\frac{mg}{S}$

lo que da

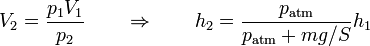
$V_2 = \frac{p_1V_1}{p_2}\qquad\Rightarrow\qquad h_2 = \frac{p_\mathrm{atm}}{p_\mathrm{atm}+mg/S}h_1$

Este resultado es el mismo tanto si el peso se coloca de una vez como si se coloca gradualmente en forma de granos de arena.

El valor del trabajo, en cambio, es diferente en cada caso.

5.1 Descenso con una pesa

Cuando se coloca un peso unitario de 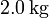$2.0\,\mathrm{kg}$ la presión externa aumenta bruscamente de $p 1$ a $p 2$ y a partir de ahí permanece constante. La presión interior, en cambio, no sabemos cuanto vale, pues en el descenso brusco del pistón el gas no se encuentra en equilibrio y la presión variará de un punto a otro de la cámara. Esto no es problema, ya que el trabajo sobre el gas se calcula empleando la presión externa

$W = -\int_{V_1}^{V_2}p_\mathrm{ext}\,\mathrm{d}V$

Como la presión externa es constante, se puede sustituir y sacar de la integral

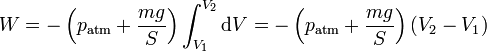
$W = -\left(p_\mathrm{atm}+\frac{mg}{S}\right)\int_{V_1}^{V_2}\mathrm{d}V = -\left(p_\mathrm{atm}+\frac{mg}{S}\right)(V_2-V_1)$

Teniendo en cuenta que el primer factor es $p 2$ , la presión final, esto se puede escribir, con ayuda de la ley de Boyle $p 1 V 1 = p 2 V 2$

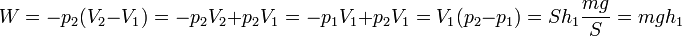
$W = -p_2(V_2-V_1) = -p_2V_2+p_2V_1 = -p_1V_1+p_2V_1 = V_1(p_2-p_1) = Sh_1\frac{mg}{S}=mgh_1$

El valor numérico de este trabajo es

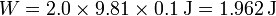
$W = 2.0\times 9.81\times 0.1\,\mathrm{J} = 1.962\,\mathrm{J}$

5.2 Descenso acumulando arena

En el segundo caso, la presión exterior no es constante, sino que va variando a medida que se va añadiendo arena. Una forma de resolver este apartado sería suponer que para una presión dada, se añade un grano de arena de masa $d m$ , lo que reduce el volumen una cantidad diferencial, según la fórmula del apartado anterior.

Sin embargo, es más fácil observar que si la presión se aumenta muy lentamente al gas le da tiempo a alcanzar el equilibrio térmico con el exterior, por lo que se trata de un proceso cuasiestático a temperatura constante. En este caso la presión interna del gas es igual a la exterior y el trabajo se puede hallar empleando la presión interior

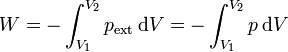
$W = -\int_{V_1}^{V_2}p_\mathrm{ext}\,\mathrm{d}V = -\int_{V_1}^{V_2}p\,\mathrm{d}V$

y puesto que la temperatura permanece constante se cumple en todo momento

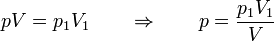
$pV=p_1V_1 \qquad\Rightarrow\qquad p=\frac{p_1V_1}{V}$

Llevando esto a la integral

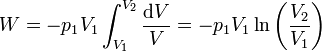
$W = -p_1V_1\int_{V_1}^{V_2}\frac{\mathrm{d}V}{V}=-p_1V_1\ln\left(\frac{V_2}{V_1}\right)$

Aplicando de nuevo la ley de Boyle podemos escribir esto en términos del cociente entre presiones en lugar de volúmenes

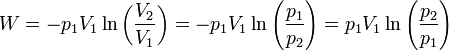
$W = -p_1V_1\ln\left(\frac{V_2}{V_1}\right)=-p_1V_1\ln\left(\frac{p_1}{p_2}\right)=p_1V_1\ln\left(\frac{p_2}{p_1}\right)$

Sustituyendo los valores numéricos

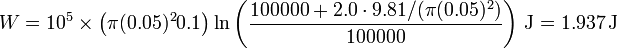
$W = 10^5\times \left(\pi (0.05)^2 0.1\right)\ln\left(\frac{100000+2.0\cdot 9.81/(\pi(0.05)^2)}{100000}\right)\,\mathrm{J}=1.937\,\mathrm{J}$

Vemos que el trabajo en ambos casos es positivo, como corresponde a una compresión, pero en el segundo caso es un poco menor que en el primero

6 Energía interna

La energía interna de un gas ideal es una función de estado que depende exclusivamente de la temperatura. En este problema, para cualquiera de los dos procesos la temperatura final es la misma que la inicial y por tanto la energía interna tiene incremento nulo

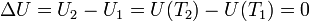
$\Delta U = U_2-U_1 = U(T_2)-U(T_1) = 0\,$

7 Calor

De acuerdo con el primer principio de la termodinámica la suma del trabajo y el calor que entran en un sistema nos dan la variación de la energía interna

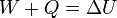
$W+Q=\Delta U\,$

En este caso, sabemos que la variación de la energía interna es nula, por lo que

$\Delta U = 0\qquad \Rightarrow\qquad Q = - W$

Esto quiere decir que toda la energía que introducimos en el sistema en forma de trabajo escapa por las paredes en forma de calor. Al comprimir el gas se calienta (muy poco si el proceso es cuasiestático; una cantidad finita si se trata de una compresión abrupta). Se produce entonces una diferencia de temperatura con el exterior, que genera un flujo de calor hacia afuera.

El valor numérico del calor será el mismo que el del trabajo que calculamos antes, con signo opuesto.

Descenso con una pesa

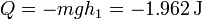
$Q = -mgh_1 = -1.962\,\mathrm{J}$

Descenso con un montón de arena

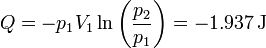
$Q = -p_1V_1\ln\left(\frac{p_2}{p_1}\right)=-1.937\,\mathrm{J}$

El signo negativo implica que el calor sale del sistema.

Trabajo en una compresión por un peso

De Laplace

Contenido

1 Enunciado

2 Introducción

3 Caso isotermo

4 Caso adiabático

5 Trabajo

5.1 Descenso con una pesa

5.2 Descenso acumulando arena

6 Energía interna

7 Calor

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES