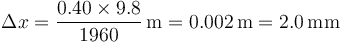Masa que cae sobre resorte

De Laplace

1 Enunciado

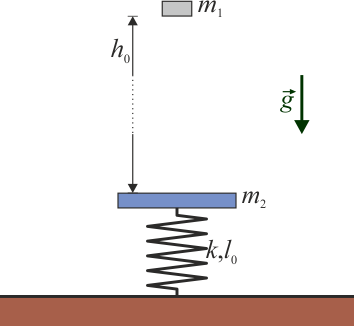
Se tiene una plataforma de masa 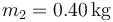situada sobre un resorte de constante 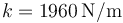y longitud natural .

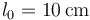1. Calcule cuánto se comprime el resorte debido al peso de la masa, en la posición de equilibrio.

Sobre esta plataforma se deja caer una masa , soltándola sin velocidad inicial desde una altura 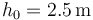sobre la plataforma

2. Calcule la velocidad que tiene la masa m₁ justo antes de impactar con la plataforma.

Si la colisión es perfectamente elástica,

3. Calcule la nueva altura que alcanza la masa m₁ tras la colisión.
4. Calcule cuánto es el máximo que se comprime el resorte por efecto del golpe en la plataforma.

Si la colisión, en vez de ser elástica, es completamente inelástica,

5. ¿Cuánta energía se pierde en la colisión?
6. ¿Cuánto se comprime como máximo el resorte tras la colisión?

Tómese .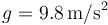

2 Compresión del resorte

Puesto que todas las fuerzas y velocidades van a ser verticales, el problema es unidimensional y podemos emplear cantidades escalares con signo. Consideraremos una velocidad y una fuerza como positivas cuando van hacia abajo y negativas si van hacia arriba.

La presencia de la masa comprime el muelle por acción de su peso. En el equilibrio se compensa la acción del peso con la fuerza recuperadora elástica:

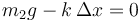
lo que da la compresión del muelle

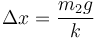
Sustituyendo los valores numéricos

3 Velocidad de impacto

4 Nueva altura máxima

5 Máxima compresión

6 Energía disipada

7 Máxima compresión en el caso inelástico