Oscilador armónico tridimensional

De Laplace

1 Enunciado

Una partícula se mueve en tres dimensiones de forma tal que verifica la ecuación del oscilador armónico

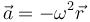
con 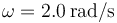. Su posición inicial es .

1. Para el caso 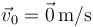. ¿Qué tipo de movimiento describe la partícula?
2. Para el caso , ¿cómo es la trayectoria? ¿Qué tipo de movimiento describe la partícula?
3. Suponga ahora que , ¿cómo es ahora la trayectoria de la partícula?
4. Para los tres casos anteriores, determine

1. la rapidez,
2. las componentes intrínsecas de la aceleración,
3. los vectores tangente y normal,
4. el radio de curvatura y el centro de curvatura.

para los instantes 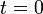, 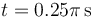y .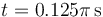

2 Solución general

La solución general de la ecuación del oscilador armónico en 3D es de la forma

3 Caso v₀ = 0 m/s

4 Caso v₀ = 10 m/s

5 Caso v₀ = 8 m/s

6 Cálculo de magnitudes

6.1 Rapidez

6.2 Componentes de la aceleración

6.3 Vectores tangente y normal

6.4 Racio y centro de curvatura