Movimiento circular en 3D
De Laplace
Revisión a fecha de 18:08 7 nov 2013; Antonio (Discusión | contribuciones)
1 Enunciado
Una partícula se mueve según las ecuaciones horarias
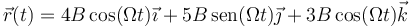
con B y Ω constantes.
- ¿Qué trayectoria sigue la partícula?
- ¿Qué desplazamiento realiza y qué distancia recorre la partícula entre t=0 y t = π/Ω?
- ¿Qué tipo de movimiento describe la partícula?
2 Trayectoria
Podemos identificar la trayectoria a partir de razonamientos puramente geométricos o empleando procedimientos cinemáticos.
2.1 Identificación geométrica
Si separamos las tres componentes del movimiento