Análisis de ecuación horaria

De Laplace

Revisión a fecha de 17:03 5 nov 2013; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Desplazamiento y distancia
- 2.1 Desplazamiento
- 2.2 Distancia
3 Componentes intrínsecas de la aceleración
4 Radio y centro de curvatura

1 Enunciado

Una partícula se mueve por el espacio de forma que su posición, en las unidades fundamentales del SI, viene dada por la ecuación horaria

$\vec{r}=t^2\vec{\imath}+t\vec{\jmath}+\frac{2}{3}t^3\vec{k}$

Calcule el desplazamiento y la distancia que recorre la partícula entre t = 0 y t = 3 s.
Halle las componentes intrínsecas de la aceleración en t = 2 s, como escalares y como vectores.
Calcule el radio de curvatura en t = 2 s así como el centro de curvatura en ese instante.

2 Desplazamiento y distancia

2.1 Desplazamiento

El desplazamiento lo da la diferencia (vectorial) entre la posición final y la inicial

$\Delta \vec{r}=\vec{r}(3\,\mathrm{s})-\vec{r}(1\,\mathrm{s})$

Sustituyendo en la ecuación horaria

$\vec{r}(1\,\mathrm{s})=(\vec{\imath}+\vec{\jmath}+\frac{2}{3}\vec{k})\,\mathrm{m}\qquad\qquad \vec{r}(3\,\mathrm{s})=(9\vec{\imath}+3\vec{\jmath}+18\vec{k})\,\mathrm{m}$

resulta el desplazamiento

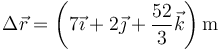
$\Delta \vec{r}=\left(7\vec{\imath}+2\vec{\jmath}+\frac{52}{3}\vec{k}\right)\mathrm{m}$

El módulo de este desplazamiento vale

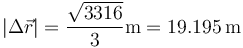
$\left|\Delta\vec{r}\right|=\frac{\sqrt{3316}}{3}\mathrm{m}=19.195\,\mathrm{m}$

2.2 Distancia

Para hallar la distancia recorrida debemos calcular en primer lugar la rapidez, ya que

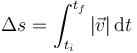
$\Delta s = \int_{t_i}^{t_f}\left|\vec{v}\right|\mathrm{d}t$

Calculamos en primer lugar la velocidad

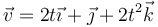
$\vec{v}=2t\vec{\imath}+\vec{\jmath}+2t^2\vec{k}$

A partir de esta la rapidez

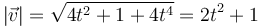
$\left|\vec{v}\right| = \sqrt{4t^2+1+4t^4} = 2t^2+1$

Integramos ésta entre el instante inicial y el final

$\Delta s=\int_1^3 (2t^2+1)\mathrm{d}t=\left(\frac{2}{3}t^3+t\right|_1^3 = \frac{58}{3}\mathrm{m}=19.33\,\mathrm{m}$

La distancia recorrida es superior al módulo del desplazamiento, ya que la trayectoria es una curva, mientras que el módulo del desplazamiento se mide en línea recta, que siempre es una distancia más corta.

3 Componentes intrínsecas de la aceleración

4 Radio y centro de curvatura

Análisis de ecuación horaria

De Laplace

Contenido

1 Enunciado

2 Desplazamiento y distancia

2.1 Desplazamiento

2.2 Distancia

3 Componentes intrínsecas de la aceleración

4 Radio y centro de curvatura

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES