Entrar Página Discusión Historial Go to the site toolbox

Análisis de ecuación horaria

De Laplace

Contenido

1 Enunciado

Una partícula se mueve por el espacio de forma que su posición, en las unidades fundamentales del SI, viene dada por la ecuación horaria

\vec{r}=t^2\vec{\imath}+t\vec{\jmath}+\frac{2}{3}t^3\vec{k}
  1. Calcule el desplazamiento y la distancia que recorre la partícula entre t = 0 y t = 3 s.
  2. Halle las componentes intrínsecas de la aceleración en t = 2 s, como escalares y como vectores.
  3. Calcule el radio de curvatura en t = 2 s así como el centro de curvatura en ese instante.

2 Desplazamiento y distancia

2.1 Desplazamiento

El desplazamiento lo da la diferencia (vectorial) entre la posición final y la inicial

\Delta \vec{r}=\vec{r}(3\,\mathrm{s})-\vec{r}(1\,\mathrm{s})

Sustituyendo en la ecuación horaria

\vec{r}(1\,\mathrm{s})=(\vec{\imath}+\vec{\jmath}+\frac{2}{3}\vec{k})\,\mathrm{m}\qquad\qquad \vec{r}(3\,\mathrm{s})=(9\vec{\imath}+3\vec{\jmath}+18\vec{k})\,\mathrm{m}

resulta el desplazamiento

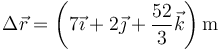
\Delta \vec{r}=\left(7\vec{\imath}+2\vec{\jmath}+\frac{52}{3}\vec{k}\right)\mathrm{m}

El módulo de este desplazamiento vale

\left|\Delta\vec{r}\right|=\frac{\sqrt{3316}}{3}mathrm{m}=19.195\,\mathrm{m}

3 Componentes intrínsecas de la aceleración

4 Radio y centro de curvatura

Obtenido de "http://tesla.us.es/wiki/index.php/An%C3%A1lisis_de_ecuaci%C3%B3n_horaria"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace