Campo eléctrico en el eje de un anillo

De Laplace

Revisión a fecha de 20:07 29 nov 2008; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Solución

1 Enunciado

Halle el campo eléctrico en todos los puntos del eje de un anillo de radio $R$ sobre el cual hay una densidad de carga uniforme $λ$ .

A partir de este resultado, calcule el campo creado por una corona circular de radios $R 1$ y $R 2$ ( $R 1 < R 2$ ), sobre la cual hay una densidad de carga uniforme $σ 0$ , en los puntos de su eje.

¿A que se reduce si 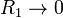$R_1\to 0$ ? ¿Y si 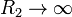$R_2\to\infty$ ? Considere en particular el comportamiento en las proximidades de $z = 0$ .

2 Solución

2.1 Campo de un anillo uniforme

La expresión general para el campo creado por una distribución lineal de carga es

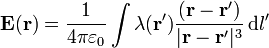
$\mathbf{E}(\mathbf{r})=\frac{1}{4\pi\varepsilon_0}\int \lambda(\mathbf{r}')\frac{ (\mathbf{r}-\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|^3}\,\mathrm{d}l'$

En general, la densidad lineal $λ$ es una función de la posición. En este caso, se trata de una distribución uniforme y puede salir de la integral.

Deseamos calcular el campo eléctrico exclusivamente en los puntos del eje, que tomaremos como eje $Z$ , con lo que

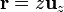
$\mathbf{r}=z\mathbf{u}_{z}$

Por su parte, podemos parametrizar los puntos del anillo como

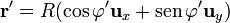
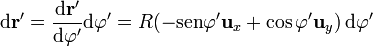
$\mathbf{r}'=R(\cos\varphi'\mathbf{u}_{x}+\mathrm{sen}\,\varphi'\mathbf{u}_{y})$ $\mathrm{d}\mathbf{r}'=\frac{\mathrm{d}\mathbf{r}'}{\mathrm{d}\varphi'}\mathrm{d}\varphi'=R(-\mathrm{sen}\varphi'\mathbf{u}_{x}+\cos\varphi'\mathbf{u}_{y})\,\mathrm{d}\varphi'$ $\mathrm{d}l'=|\mathrm{d}\mathbf{r}'|=R\,\mathrm{d}\varphi'$

y la distancia del punto de medida a la posición de las fuentes, igual para todos los puntos del anillo

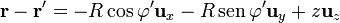
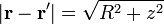
$\mathbf{r}-\mathbf{r}'=-R\cos\varphi'\mathbf{u}_{x}-R\,\mathrm{sen}\,\varphi'\mathbf{u}_{y}+z\mathbf{u}_{z}$ $|\mathbf{r}-\mathbf{r}'|=\sqrt{R^2+z^2}$

El campo nos queda entonces

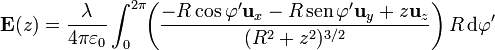
$\mathbf{E}(z)=\frac{\lambda}{4\pi\varepsilon_0}\int_0^{2\pi}\!\! \left(\frac{-R\cos\varphi'\mathbf{u}_{x}-R\,\mathrm{sen}\,\varphi'\mathbf{u}_{y}+z\mathbf{u}_{z}}{(R^2+z^2)^{3/2}}\right)R\,\mathrm{d}\varphi'$

Las componentes en $x$ e $y$ se anulan al integrar sobre un periodo, de forma que el campo sólo posee componente en la dirección $z$ . Este resultado es previsible a la vista de otros problemas con sistemas simétricos. Para cada punto del anillo existe uno diametralmente opuesto cuyas componentes $x$ e $y$ del campo anulan a las del primero. Esto nos deja sólo con la componente $z$ que además no depende de $\varphi$ , y que podemos integrar trivialmente

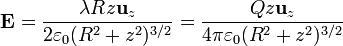
$\mathbf{E}=\frac{\lambda R z \mathbf{u}_{z}}{2\varepsilon_0 (R^2+z^2)^{3/2}}= \frac{Qz\mathbf{u}_{z}}{4\pi\varepsilon_0 (R^2+z^2)^{3/2}}$

con $Q = 2π R λ$ la carga total. Este campo posee una dependencia en $z$ como la ilustrada en la figura. Justo en el punto central el campo es nulo. Al aumentar $z$ crece, para luego disminuir a medida que nos alejamos del anillo y de su influencia.

Cuando 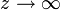$z\to\infty$ el campo tiende a

$\mathbf{E}\to \frac{\lambda R z \mathbf{u}_{z}}{2\varepsilon_0|z|^3}=\frac{1}{4\pi\varepsilon_0}\,\frac{Q \mathbf{r}}{r^3}$

Según esto, si nos situamos puntos muy alejados del anillo, su tamaño pasa a ser despreciable y lo percibimos simplemente como una carga puntual.

2.2 Campo de una corona

Nuestro siguiente problema es el de una corona circular de radio interior $R 1$ y exterior $R 2$ . Podemos considerar esta corona como compuesta de anillos concéntricos, al estilo de aros de cebolla. Cada uno de estos anillos tendrá un cierto radio $ρ'$ y un cierto espesor $dρ'$ . Podemos sumar el campo de los diferentes anillos para obtener el campo de la corona completa. El campo de cada anillo será

$d\mathbf{E} = \frac{dQ\,z\mathbf{u}_{z}}{4\pi\varepsilon_0(\rho'^2+z^2)^{3/2}}$

donde la carga $d Q$ es la cantidad de carga, diferencial, contenida en el anillo. La obtenemos sabiendo que la densidad de carga de la corona es uniforme y que el área del anillo equivale a su longitud por su anchura

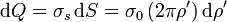
$\mathrm{d}Q=\sigma_s\,\mathrm{d}S= \sigma_0\,(2\pi\rho')\,\mathrm{d}\rho'$

El campo de la corona será entonces

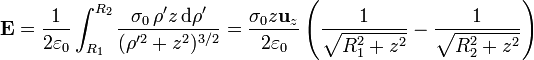
$\mathbf{E}=\frac{1}{2\varepsilon_0}\int_{R_1}^{R_2}\frac{\sigma_0\,\rho'z\,\mathrm{d}\rho'} {(\rho'^2+z^2)^{3/2}}=\frac{\sigma_0 z\mathbf{u}_{z}}{2\varepsilon_0} \left(\frac{1}{\sqrt{R_1^2+z^2}}-\frac{1}{\sqrt{R_2^2+z^2}}\right)$

Este campo es válido para toda corona circular. En la gráfica tenemos el resultado para $R 2 = 2 R 1$ .

2.3 Campo de un disco y de un plano

Campo eléctrico en el eje de un anillo

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Campo de un anillo uniforme

2.2 Campo de una corona

2.3 Campo de un disco y de un plano

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES