Entrar Página Discusión Historial Go to the site toolbox

Partícula ensartada en un aro circular (GIA)

De Laplace

Revisión a fecha de 09:27 30 oct 2013; Pedro (Discusión | contribuciones)
(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado

Se tiene un aro circular de radio R. Engarzado en él hay una masa m que puede deslizar siguiendo la circunferencia del aro bajo la acción de la gravedad.

  1. Suponiendo que el contacto es liso, encuentra las ecuaciones que describen el movimiento de la masa en función del ángulo α de la figura.
  2. Soltamos la masa con velocidad inicial nula y un ángulo inicial 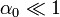\alpha_0\ll1. Encuentra la función α(t) que describe el movimiento de la masa.
  3. Supongamos ahora que nos dicen que la masa realiza un movimiento circular uniforme con frecuencia angular Ω. Encuentra la expresión de la fuerza de ligadura en función del ángulo θ. ¿Es constante? En este caso, ¿el vínculo es liso o rugoso?

2 Solución

2.1 Ecuaciones de movimiento

Tenemos una partícula vinculada, pues está obligada a moverse siguiendo la circunferencia del aro. Se trata de un vínculo bilateral, geométrico (no aparece la velocidad) y esclerónomo (no aparece explícitamente el tiempo pues el aro no se mueve). Nos dice el enunciado que es además liso, esto es, la fuerza de reacción vincular que sustituye a la ligadura es perpendicular a la superficie del anillo. Las ecuaciones que definen el vínculo son las de una circunferencia de radio R, en el plano OXY y centrada en el origen de coordenadas O:

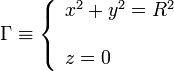
\Gamma\equiv \left\{ \begin{array}{l} x^2+y^2=R^2\\ \\ z=0 \end{array} \right.

Hemos escrito las ecuaciones en coordenadas cartesianas, usando el sistema de ejes de la figura.

Como hay dos ecuaciones vinculares, y una partícula libre tiene 3 grados de libertad, el número de grados de libertad del problema es r = 3 − 2 = 1. Por tanto, basta con un parámetro para describir la posición de la partícula. Usaremos el ángulo θ(t).

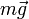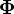Las fuerzas que actúan sobre la partícula son el peso m\vec{g}, que es la fuerza activa, y la fuerza de reacción vincular \boldsymbol{\Phi}, que sustituye al vínculo. La ecuación de movimiento de la partícula se obtiene de la Segunda Ley de Newton teniendo sustituyendo el vínculo por la fuerza de reacción vincular

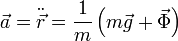
\vec{a} = \ddot{\vec{r}} = \frac{1}{m}\left(m\vec{g} + \vec{\Phi}\right)

Tenemos dos incógnitas en el problema, θ(t) y Φ(t). Necesitamos por tanto dos ecuaciones. Para obtenerlas hemos de proyectar la Segunda Ley en un sistema de ejes y convertir la ecuación vectorial en dos ecuaciones escalares. Vamos a hacerlo usando tres técnicas distintas: en el triedro intrínseco, en coordenadas polares y en los ejes cartesianos


2.1.1 Obtención de las ecuaciones de movimiento usando coordenadas polares

Artículo completo: Coordenadas polares

En coordenadas polares los vectores de posición, velocidad y aceleración de la partícula son

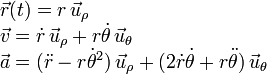
\begin{array}{l} \vec{r}(t) = r\,\vec{u}_{\rho} \\ \vec{v} = \dot{r}\,\vec{u}_{\rho} + r\dot{\theta}\,\vec{u}_{\theta}\\ \vec{a} = (\ddot{r} - r\dot{\theta}^2)\,\vec{u}_{\rho} + (2\dot{r}\dot{\theta}+r\ddot{\theta})\,\vec{u}_{\theta} \end{array}

En nuestro caso la coordenada radial es constante, pues se la partícula se mueve sobre una circunferencia. Por tanto, r = R y 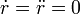\dot{r}=\ddot{r}=0 . La velocidad y aceleración quedan

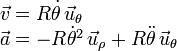
\begin{array}{l} \vec{v} = R\dot{\theta}\,\vec{u}_{\theta} \\ \vec{a} = -R\dot{\theta}^2\,\vec{u}_{\rho} + R\ddot{\theta}\,\vec{u}_{\theta} \end{array}

Como se observa en la figura las proyecciones de la fuerza de reacción vincular y la aceleración de la gravedad en los vectores de la base en polares son

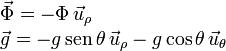
\begin{array}{l} \vec{\Phi} = -\Phi\,\vec{u}_{\rho}\\ \vec{g} = -g \,\mathrm{sen}\,\theta\,\vec{u}_{\rho} - g\cos\theta\,\vec{u}_{\theta} \end{array}

El signo menos en la fuerza de reacción vincular es para que el signo de Φ coincida con el de la proyección en el triedro intrínseco.

2.1.2 Obtención de las ecuaciones de movimiento proyectando en el triedro intrínseco

La trayectoria que sigue la partícula es una circunferencia. Podemos calcular los vectores que forman el triedro intrínseco en cada punto de la circunferencia. El vector de posición de un punto de la circunferencia parametrizado en función de θ es

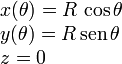
\begin{array}{l} x(\theta) = R\,\cos\theta\\ y(\theta) = R\,\mathrm{sen}\,\theta\\ z=0 \end{array}

El vector tangente es

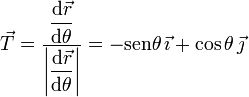
\vec{T} = \frac{\displaystyle\frac{\mathrm{d}\vec{r}}{\mathrm{d}\theta}}{\left|\displaystyle\frac{\mathrm{d}\vec{r}}{\mathrm{d}\theta}\right|} = -\mathrm{sen}\theta\,\vec{\imath} + \cos\theta\,\vec{\jmath}

El vector tangente apunta en la dirección en que varía \vec{T} . Por tanto

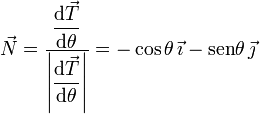
\vec{N} = \frac{\displaystyle\frac{\mathrm{d}\vec{T}}{\mathrm{d}\theta}}{\left|\displaystyle\frac{\mathrm{d}\vec{T}}{\mathrm{d}\theta}\right|} = -\cos\theta\,\vec{\imath} - \mathrm{sen}\theta\,\vec{\jmath}

La figura muestra la dirección y sentido del triedro intrínseco para un valor del ángulo θ. Debemos proyectar en esta base los dos términos de la Segunda ley. Para la aceleración utilizamos los resultados que hemos obtenido para el movimiento circular

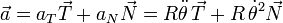
\vec{a} = a_T\vec{T} + a_N\vec{N} = R\ddot{\theta}\,\vec{T} + R\,\dot{\theta}^2\vec{N}

Como el vínculo es liso, la fuerza de reacción vincular es perpendicular al aro. Por tanto

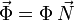
\vec{\Phi} = \Phi\,\vec{N}

No hay que olvidar que la componente Φ puede ser positiva o negativa. En el dibujo tendría un valor negativo. Por último, de la figura vemos que la aceleración de la gravedad se proyecta en el triedro intrínseco como

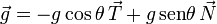
\vec{g} = -g\cos\theta\,\vec{T} + g\,\mathrm{sen}\theta\,\vec{N}

A partir de la Segunda Ley (ecuación vectorial) obtenemos dos ecuaciones escalares (una de las componentes en \vec{T} y otra de las componentes en \vec{N}

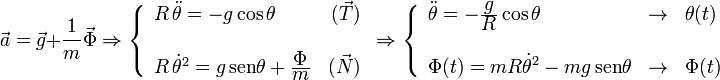
\vec{a} = \vec{g} +\frac{1}{m}\vec{\Phi} \Rightarrow \left\{ \begin{array}{lr} R\,\ddot{\theta} = -g\cos\theta & (\vec{T}) \\ &\\ R\,\dot{\theta}^2 = g\,\mathrm{sen}\theta + \frac{\displaystyle \Phi}{\displaystyle m}&(\vec{N}) \end{array} \right. \Rightarrow \left\{ \begin{array}{lcl} \ddot{\theta} = -\frac{\displaystyle g}{\displaystyle R}\cos\theta & \to &\theta(t) \\ &&\\ \Phi(t) = mR\dot{\theta}^2 - mg\,\mathrm{sen}\theta & \to &\Phi(t) \end{array} \right.

Resolviendo la primera ecuación obtendríamos θ(t) y de la segunda tendríamos la fuerza de reacción vincular Φ(t).


2.1.3 Obtención de las ecuaciones de movimiento usando coordenadas cartesianas

Por último, vamos a encontrar las ecuaciones de movimiento usando coordenadas cartesianas. Vamos a ver que este es el método que obliga a cálculos más laboriosos.

Utilizamos el ángulo θ(t) para parametrizar el movimiento. Los vectores de posición, velocidad y aceleración son

\begin{array}{l} \vec{r}(t) = \vec{r}[\theta(t)] = x[\theta(t)]\,\vec{\imath} + y[\theta(t)]\,\vec{\jmath}\\ \\ \vec{v} = \dot{\vec{r}} = \frac{\displaystyle \mathrm{d}\vec{r}}{\displaystyle\mathrm{d}\theta} \frac{\displaystyle\mathrm{d}\theta}{\displaystyle\mathrm{d} t} = -R\dot{\theta}\,\mathrm{sen}\,\theta\,\vec{\imath} + R\dot{\theta}\cos\theta\,\vec{\jmath}\\ \\ \vec{a} = \dot{\vec{v}} = \dfrac{\partial \vec{r}}{\partial \theta}\,\dot{\theta}+\dfrac{\partial \vec{r}}{\partial \dot{\theta}}\,\ddot{\theta} = (-R\ddot{\theta}\,\mathrm{sen}\,\theta-R\dot{\theta}^2\cos\theta)\,\vec{\imath} + (R\ddot{\theta}\cos\theta-R\dot{\theta}^2\,\mathrm{sen}\,\theta)\,\vec{\jmath} \end{array}

La expresión de la fuerza de reacción vincular y la aceleración de la gravedad en los vectores de la base cartesianas es

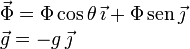
\begin{array}{l} \vec{\Phi} = \Phi\cos\theta\,\vec{\imath} + \Phi\,\mathrm{sen}\,\vec{\jmath} \\ \vec{g} = -g\,\vec{\jmath} \end{array}

Escribimos la Segunda Ley de Newton en coordenadas cartesianas e igualamos componente a componente

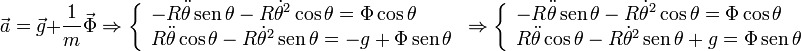
\vec{a} = \vec{g}+\frac{1}{m}\vec{\Phi} \Rightarrow \left\{ \begin{array}{l} -R\ddot{\theta}\,\mathrm{sen}\,\theta-R\dot{\theta}^2\cos\theta = \Phi\cos\theta \\ R\ddot{\theta}\cos\theta-R\dot{\theta}^2\,\mathrm{sen}\,\theta = -g + \Phi\,\mathrm{sen}\,\theta \end{array} \right. \Rightarrow \left\{ \begin{array}{l} -R\ddot{\theta}\,\mathrm{sen}\,\theta-R\dot{\theta}^2\cos\theta = \Phi\cos\theta \\ R\ddot{\theta}\cos\theta-R\dot{\theta}^2\,\mathrm{sen}\,\theta +g = \Phi\,\mathrm{sen}\,\theta \end{array} \right.

Dividiendo una ecuación por la otra y multiplicando en aspa tenemos

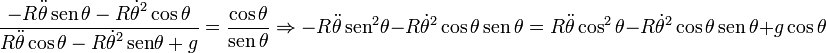
\frac{\displaystyle -R\ddot{\theta}\,\mathrm{sen}\,\theta-R\dot{\theta}^2\cos\theta} {\displaystyle R\ddot{\theta}\cos\theta-R\dot{\theta}^2\,\mathrm{sen}\theta +g} =\frac{\displaystyle \cos\theta}{\displaystyle \mathrm{sen}\,\theta} \Rightarrow -R\ddot{\theta}\,\mathrm{sen}^2\theta - R\dot{\theta}^2\cos\theta\,\mathrm{sen}\,\theta =R\ddot{\theta}\cos^2\theta - R\dot{\theta}^2\cos\theta\,\mathrm{sen}\,\theta + g\cos\theta

El término con 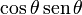\cos\theta\,\mathrm{sen}\,\theta a ambos lados de la igualdad. Utilizando la igualdad sen2θ + cos2θ = 1 llegamos de nuevo a la ecuación

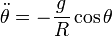
\ddot{\theta} = -\frac{\displaystyle g}{\displaystyle R}\cos\theta

La expresión para Φ(t) se obtiene despejando en las ecuaciones.

2.2 Resolución de la ecuación de movimiento

La ecuación diferencial que define el movimiento es

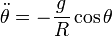
\ddot{\theta} = -\frac{\displaystyle g}{\displaystyle R}\cos\theta

Para resolver el problema, necesitaríamos dos condiciones iniciales, por ejemplo, un ángulo inicial θ0 y una velocidad inicial v0. A partir de la expresión de la velocidad en coordenadas polares vemos que una condición sobre la velocidad se convierte en una condición sobre 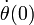\dot{\theta}(0)

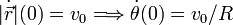
|\dot{\vec{r}}|(0)=v_0\Longrightarrow \dot{\theta}(0)=v_0/R

De este modo el problema se plantearía como

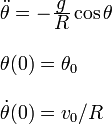
\begin{array}{l} \ddot{\theta} = -\frac{\displaystyle g}{\displaystyle R}\cos\theta\\ \\ \theta(0)=\theta_0\\ \\ \dot{\theta}(0)=v_0/R \end{array}

Este problema no se puede resolver en términos de funciones elementales. En el siguiente apartado veremos un límite en el que el problema sí es resoluble. Para ello, vamos a describir el movimiento en función del ángulo α de la figura. Tenemos

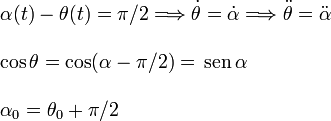
\begin{array}{l} \alpha(t) -\theta(t)=\pi/2\Longrightarrow \dot{\theta}=\dot{\alpha} \Longrightarrow\ddot{\theta}=\ddot{\alpha}\\ \\ \cos\theta=\cos(\alpha-\pi/2)=\,\mathrm{sen}\,\alpha\\ \\ \alpha_0=\theta_0+\pi/2 \end{array}

Por tanto el problema en términos de α(t) queda planteado como

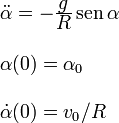
\begin{array}{l} \ddot{\alpha} = -\frac{\displaystyle g}{\displaystyle R}\,\mathrm{sen}\,\alpha\\ \\ \alpha(0)=\alpha_0\\ \\ \dot{\alpha}(0)=v_0/R \end{array}

2.3 Caso de ángulo 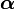\boldsymbol{\alpha} pequeño

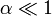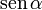Si nos restringimos al caso \alpha\ll1, el problema tiene solución sencilla. Usando el desarrollo de Maclaurin (es decir, el desarrollo de Taylor cerca de α = 0), la función \,\mathrm{sen}\,\alpha en las proximidades de α = 0 se puede expresar como

\,\mathrm{sen}\,\alpha=\left.\,\mathrm{sen}\,\alpha\right|_{\alpha=0} +\left.\frac{\mathrm{d}(\,\mathrm{sen}\,\alpha)}{\mathrm{d}\alpha}\right|_{\alpha=0}\alpha+O(\alpha^2)

Por tanto, despreciando términos de orden superior obtenemos

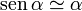
\,\mathrm{sen}\,\alpha\simeq\alpha

Nos dice el enunciado que la partícula parte del reposo (v0 = 0) y con un ángulo inicial α0. El problema queda

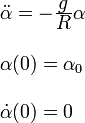
\begin{array}{l} \ddot{\alpha}=-\frac{\displaystyle g}{\displaystyle R}\alpha\\ \\ \alpha(0)=\alpha_0\\ \\ \dot{\alpha}(0)=0 \end{array}

Buscamos soluciones de la forma

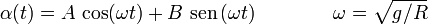
\alpha(t)=A\,\cos(\omega t)+B\,\,\mathrm{sen}\,(\omega t)\qquad\qquad\omega=\sqrt{g/R}

Imponiendo las condiciones iniciales obtenemos que el ángulo α(t) viene dado por

\alpha(t)=\alpha_0\cos(\omega t)\qquad\qquad\omega=\sqrt{g/R}

Esto quiere decir que la partícula realiza oscilaciones de amplitud α0 alrededor del punto más bajo del aro, y con un período

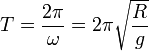
T = \frac{2\pi}{\omega}=2\pi\sqrt{\frac{R}{g}}

2.4 Movimiento circular uniforme

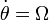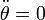En este caso el dato es el movimiento. Se nos dice que la partícula recorre el aro con un movimiento circular uniforme de frecuencia angular \dot{\theta}=\Omega. Por tanto la aceleración angular es \ddot{\theta}=0. Con esto podemos determinar su posición, velocidad y aceleración en función del tiempo.

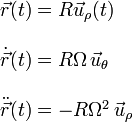
\begin{array}{l} \vec{r}(t) = R\vec{u}_{\rho}(t)\\ \\ \dot{\vec{r}}(t)=R\Omega\,\vec{u}_{\theta}\\ \\ \ddot{\vec{r}}(t)=-R\Omega^2\,\vec{u}_{\rho} \end{array}

Y ahora usamos la Segunda Ley de Newton para determinar la fuerza de reacción vincular en función de la posición de la partícula

\begin{array}{l} m\ddot{\vec{r}}=m\vec{g}+\boldsymbol{\Phi}\Rightarrow \boldsymbol{\Phi}=m\ddot{\vec{r}}-m\vec{g} \\ \\ \boldsymbol{\Phi} = m(g\,\mathrm{sen}\,\theta-R\Omega^2)\,\vec{u}_{\rho}+mg\cos\theta\,\vec{u}_{\theta} \end{array}

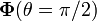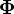En la figura se muestra la fuerza de reacción vincular para cuatro posiciones de la partícula. En este caso se tiene RΩ2 > g, por lo que \boldsymbol{\Phi}(\theta=\pi/2) apunta hacia abajo. Puede observarse que \boldsymbol{\Phi} tiene componente tangencial, por lo que el vínculo sería rugoso.


2.5 Comentarios sobre el caso de ángulo 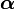\boldsymbol{\alpha} grande

En el segundo apartado hemos visto la solución para ángulo pequeño. Decíamos que cuando el ángulo es pequeño la función sinα se puede sustituir por α. Podemos preguntarnos que quiere decir pequeño . La respuesta está en el desarrollo de Taylor de 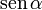\,\mathrm{sen}\,\alpha. Incluyendo los dos primeros términos este desarrollo es

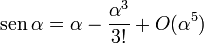
\,\mathrm{sen}\,\alpha=\alpha-\frac{\alpha^3}{3!}+O(\alpha^5)

Al despreciar el segundo término estamos imponiendo la condición

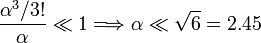
\frac{\alpha^3/3!}{\alpha}\ll1\Longrightarrow \alpha\ll\sqrt{6}=2.45

Si imponemos por ejemplo que 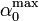\alpha_0^{\mathrm{max}} sea el 10% ese valor límite, obtenemos un valor máximo del ángulo

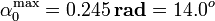
\alpha_0^{\mathrm{max}}=0.245\,\mathbf{rad}=14.0^o

La gráfica adjunta muestra la función 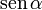\,\mathrm{sen}\,\alpha y α en las proximidades de α = 0. Puede observarse que para 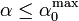\alpha\leq\alpha_0^{\mathrm{max}} las dos funciones son prácticamente iguales.

Podemos también resolver numéricamente el problema para un ángulo cualquiera y comparar las soluciones. Como condición inicial vamos a situar la partícula en el punto mas bajo del aro, e ir variando la velocidad inicial. Para valores pequeños de ésta, la amplitud de oscilación será pequeña y se cumplirá la condición de ángulo pequeño. Para velocidades iniciales grandes la bolita sube mucho y el ángulo ya no podrá considerarse pequeño. El problema es

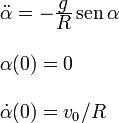
\begin{array}{l} \ddot{\alpha}=-\frac{\displaystyle g}{\displaystyle R}\,\mathrm{sen}\,\alpha\\ \\ \alpha(0)=0\\ \\ \dot{\alpha}(0)=v_0/R \end{array}

La figura muestra la evolución de α(t) para un ángulo máximo muy pequeño y otro ángulo máximo próximo a π (la partícula llega casi hasta el punto más alto del aro). En el primer caso la solución tiene forma de seno, pues se cumple 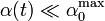\alpha(t)\ll\alpha_0^{\mathrm{max}}. En el segundo caso se ve claramente que ya no es una función seno. El ángulo está escalado con su valor máximo y el tiempo con el período correspondiente al oscilador armónico.

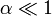En la misma gráfica se observa que, para ángulos grandes, la función sigue siendo periódica, aunque no sea senoidal. Pero su período va aumentando con el ángulo. Se puede calcular la variación del período en función del ángulo máximo alcanzado. El resultado se muestra en la gráfica de la izquierda. Para ángulos máximos pequeños, el período es el del caso \alpha\ll1 (T = T0). 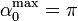Conforme se alcanzan ángulos mayores (la partícula llega más arriba) el período se va haciendo más grande, y tiende a infinito si \alpha_0^{\mathrm{max}}=\pi.

Obtenido de "http://tesla.us.es/wiki/index.php/Part%C3%ADcula_ensartada_en_un_aro_circular_(GIA)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace