Entrar Página Discusión Historial Go to the site toolbox

Calculo de magnitudes a partir de v(t)

De Laplace

Contenido

1 Enunciado

Una partícula se mueve a lo largo de una recta de forma que su velocidad sigue la ley, en el SI

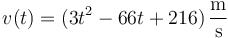
v(t) = (3t^2-66t+216)\,\frac{\mathrm{m}}{\mathrm{s}}

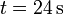entre t=0\,\mathrm{s} y t=24\,\mathrm{s}. La posición inicial es x(0) = 0\,\mathrm{m}. Halle:

  1. La posición de la partícula en cada instante del intervalo indicado.
  2. La velocidad media de la partícula en este intervalo.
  3. Los valores máximo y mínimo de x.
  4. La distancia recorrida en ese intervalo y la rapidez media.
  5. La aceleración en todo instante.
  6. Los valores máximo y mínimo de la velocidad y la rapidez.

2 Posición

La posición instantánea la hallamos integrando la velocidad

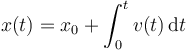
x(t) = x_0+\int_0^t v(t)\,\mathrm{d}t

En este caso

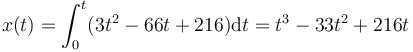
x(t) = \int_0^t(3t^2-66t + 216)\mathrm{d}t = t^3 - 33t^2 + 216t

estando el tiempo medido en segundos y la posición en metros.

3 Velocidad media

El desplazamiento en este intervalo es

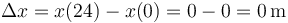
\Delta x = x(24)-x(0) = 0 - 0 = 0\,\mathrm{m}

con lo que la velocidad media es nula

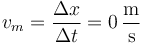
v_m = \frac{\Delta x}{\Delta t}=0\,\frac{\mathrm{m}}{\mathrm{s}}

4 Posición máxima y mínima

Los valores extremos de la posición corresponden a los instantes en que la velocidad se anula

3t^2 - 66t + 216 = 0\qquad\Rightarrow\qquad t=4\,\mathrm{s}\qquad \mbox{o}\qquad t = 18\,\mathrm{s}

siendo la posición en esos instantes

x(4\,\mathrm{s}) = 400\,\mathrm{m}\qquad\qquad x(18\,\mathrm{s})=-972\,\mathrm{m}

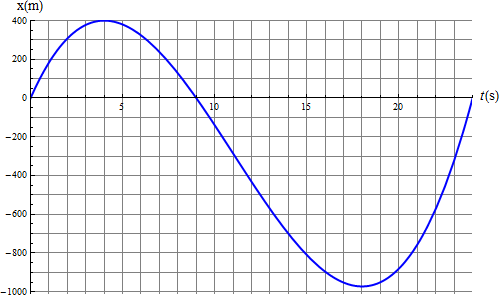
La partícula parte del origen, llega a una distancia máxima, a partir de ahí retrocede hasta un valor mínimo negativo y de ahí avanza de nuevo hasta terminar en la posición inicial

Archivo:xdet-cubica.png

5 Distancia recorrida y rapidez media

La distancia total recorrida no coincide con el desplazamiento neto, ya que la partícula va y viene en su movimiento.

De los resultados del apartado anterior tenemos que la partícula avanza 400 m, luego retrocede esos mismos 400 m y hace 972 m. Por último vuelve a recorrer de nuevo los 972 m hasta la posición original. la distancia total recorrida es

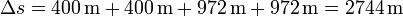
\Delta s = 400\,\mathrm{m}+400\,\mathrm{m}+972\,\mathrm{m}+972\,\mathrm{m}=2744\,\mathrm{m}

Si no hubiéramos hallado previamente estas cantidades podemos calcular la distancia total recorrida integrando la rapidez

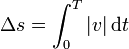
\Delta s = \int_0^T |v|\,\mathrm{d}t

El valor absoluto de la velocidad se obtiene cambiando el signo de la velocidad en los tramos en que es negativa. El cambio de signo se produce en los puntos en que la velocidad se anula.

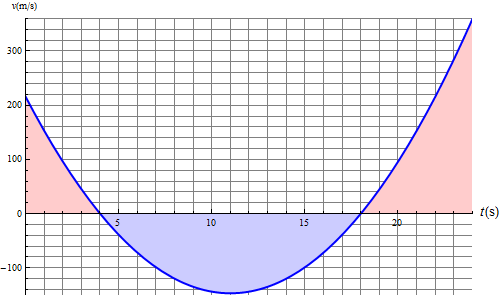
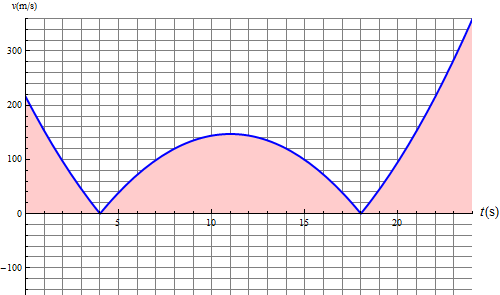
Archivo:vdet-cubica.png        Archivo:absvdet-cubica.png

Esto nos da

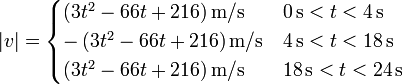
|v| = \begin{cases} \left(3t^2-66t+216\right)\mathrm{m}/\mathrm{s} & 0\,\mathrm{s} < t < 4\,\mathrm{s} \\ -\left(3t^2-66t+216\right)\mathrm{m}/\mathrm{s} & 4\,\mathrm{s} < t < 18\,\mathrm{s} \\ \left(3t^2-66t+216\right)\mathrm{m}/\mathrm{s} & 18\,\mathrm{s} < t < 24\,\mathrm{s}\end{cases}

Integrando esto

\Delta s = \int_0^4 \left(3t^2-66t+216\right)\,\mathrm{d}t-\int_4^18 \left(3t^2-66t+216\right)\,\mathrm{d}t+\int_18^24 \left(3t^2-66t+216\right)\,\mathrm{d}t = \left(400+1372+972\right)\,\mathrm{m} = 2744\,\mathrm{m}

6 Aceleración

7 Velocidad y rapidez máximas y mínimas

Obtenido de "http://tesla.us.es/wiki/index.php/Calculo_de_magnitudes_a_partir_de_v(t)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace