Entrar Página Discusión Historial Go to the site toolbox

Preguntas de test de introducción a la física (GIE)

De Laplace

Contenido

1 Longitud de un pársec

Un pársec vale, aproximadamente, 3.26 años-luz, siendo un año-luz la distancia recorrida por la luz en un año. ¿A qué equivale un pársec en el Sistema Internacional?

  • A 3.08×1013m
  • B 9.46×1015m
  • C 5.14×1014m
  • D 3.08×1016m

1.1 Solución

La respuesta correcta es la D.

Comenzamos hallando la longitud de un año-luz, para lo cual necesitamos calcular cuantos segundos hay en un año

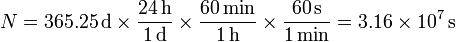
N = 365.25\,\mathrm{d}\times\frac{24\,\mathrm{h}}{1\,\mathrm{d}}\times\frac{60\,\mathrm{min}}{1\,\mathrm{h}}\times\frac{60\,\mathrm{s}}{1\,\mathrm{min}}=3.16\times 10^7\,\mathrm{s}

Multiplicando esta cantidad por la velocidad de la luz hallamos la longitud de un año luz

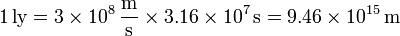
1\,\mathrm{ly}=3\times 10^8\,\frac{\mathrm{m}}{\mathrm{s}}\times 3.16\times 10^7\,\mathrm{s}=9.46\times 10^{15}\,\mathrm{m}

Como primera aproximación diríamos que un año luz son unos 10 petámetros. Exactamente vale 9.460.730.472.580,8 m.

Un pársec equivale entonces a

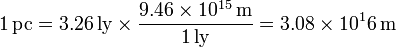
1\,\mathrm{pc}= 3.26\,\mathrm{ly}\times \frac{9.46\times 10^{15}\,\mathrm{m}}{1\,\mathrm{ly}} = 3.08\times 10^16\,\mathrm{m}

2 Velocidad de la luz

Se construye un sistema de unidades basado en el palmo (1 palmo = 20cm), el rato (1 rato = 15 minutos) y el puñado (1 puñado = 100 gramos). En este sistema, ¿cuánto vale la velocidad de la luz?

  • A 1.35 terapalmos/rato
  • B 81 terapalmos/rato
  • C 81 gigapalmos/rato
  • D 1.35 gigapalmos/rato

3 Masa de la Giralda

¿Cuál es el orden de magnitud de la masa de la Giralda?

  • A 109kg
  • B 107kg
  • C 105kg
  • D 104kg

3.1 Solución

La respuesta correcta es la B.

Podemos estimar la masa de la Giralda como el producto de su volumen por su densidad.

El volumen de la Giralda lo estimamos como el de un prisma de base cuadrada.

  • Su altura es de unos 100 m.
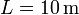  • El lado de su base estará entre unos 10 o 15 metros. Puesto que solo nos interesa el orden de magnitud suponemos L=10\,\mathrm{m}.

Esto nos da el orden de magnitud del volumen

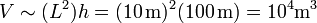
V \sim (L^2)h = (10\,\mathrm{m})^2(100\,\mathrm{m}) = 10^4\mathrm{m}^3

La densidad es más incierta ¿qué densidad tiene la piedra de que está hecha la Giralda? ¿Cómo contamos el hueco interior? Para incluir el aire, consideramos no la densidad del material, sino una densidad promedio, que será intermedia entre la de la piedra y la del aire.

Sabemos que el agua tiene una densidad de 1000 kg/m³. La piedra es más densa pero no exageradamente más densa. Incluso si fuera de oro macizo (!) su densidad sería solo 20 veces la del agua. Por tanto para estimar el orden de magnitud podemos suponer un valor promedio de 1000 kg/m³ (si fuera 2000 o 3000, ello no afectaría al orden de magnitud). Por tanto

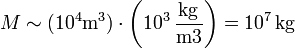
M\sim (10^4\mathrm{m}^3)\cdot\left(10^3\,\frac{\mathrm{kg}}{\mathrm{m}3}\right) = 10^7\,\mathrm{kg}

Consultando ahora una referencia exacta leemos que la masa es 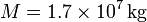M=1.7\times 10^{7}\,\mathrm{kg} (siendo el lado del cuadrado 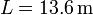L = 13.6\,\mathrm{m}) por lo cual nuestra estimación es correcta.

4 Dimensiones de constantes

Una partícula se mueve en línea recta, cumpliendo su velocidad instantánea

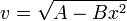
v = \sqrt{A- B x^2}

con A y B constantes positivas. ¿En que se medirá B en el SI?

  • A m−2s−2
  • B m4/s2
  • C s−2
  • D m2/s4

4.1 Solución

La respuesta correcta es la C.

Elevamos al cuadrado la ecuación, para librarnos de la raíz cuadrada

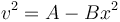
v^2 = A - B x^2\,

Las dimensiones de los tres términos deben ser las mismas

[v]^2 = [A] = [Bx^2]\,

Sustituyendo las dimensiones conocidas

\left(\frac{L}{T}\right)^2 = [A] = [B]L^2

Despejando

[B]= \frac{1}{T^2}

y por tanto en el sistema internacional su unidad es el s−2.

5 Masa de una bacteria

Una bacteria es una partícula más o menos esférica con un diámetro del orden de 1μm ¿Cuál es el orden de magnitud de la masa de una bacteria?

  • A Picogramos.
  • B Nanogramos.
  • C Femtogramos.
  • D Microgramos.

5.1 Solución

Una bacteria está hecha esencialmente de agua, por lo que la masa de una esfera de 1μm de diámetro es

No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): M = \rho V = 1000\frac{\mathrm{kg}}{\mathrm{m}^3}\left(\frac{\pi}{6}\left(10^{-6}\mathrm{m}^3\right) = \frac{\pi}6}10^{-15}\,\mathrm{kg}

La cantidad π/6 es del orden de la unidad, por lo que la masa es del orden de 10−15kg, es decir, 10−12g o usando prefijos, picogramos.

6 Cantidad de agua ingerida

¿Cual de las siguientes es una estimación más aproximada de la cantidad de agua (sola o combinada) que ingiere una persona a lo largo de su vida?

  • A 0.5 Hm³
  • B 5000 dm³
  • C 50 m³
  • D 50000 m³

7 Tamaño de una baldosa

Se mide el lado de una baldosa cuadrada y se obtiene que mide 33.3 cm. ¿Cuál es la expresión correcta de la longitud de su diagonal?

  • A: 47.1 cm
  • B 50 cm
  • C 47.09331 cm
  • D 47.0933116270 cm

7.1 Solución

La respuesta correcta es la A.

La pregunta no trata tanto del resultado del cálculo sino de su expresión. Expleando una calculadora de gran precisión obtenemos que la diagonal mide

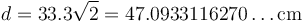
d = 33.3\sqrt{2} = 47.0933116270\ldots\mathrm{cm}

pero evidentemente es absurdo poner tantas cifras. Si el dato original procede de una medida que tiene una precisión de una décima y tiene tres cifras significativas, no puede ser que el resultado tenga 15 cifras significativas; estaríamos produciendo exactitud a partir de un dato incierto. La expresión más correcta, sin entrar en cálculos de incertidumbres, es dar tantas cifras significativas como el dato original. Redondeando queda 47.1 cm.

Obtenido de "http://tesla.us.es/wiki/index.php/Preguntas_de_test_de_introducci%C3%B3n_a_la_f%C3%ADsica_(GIE)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace