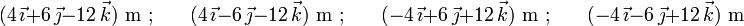1.11. Vectores con tres condiciones (Ex.Nov/11)

De Laplace

Revisión a fecha de 17:45 13 sep 2013; Enrique (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

1 Enunciado

Determine todos los vectores libres que cumplen simultáneamente las tres siguientes condiciones:

1) Tener una longitud de $14$ m.

2) Ser ortogonal al vector 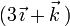$(3\,\vec{\imath}+\vec{k}\,)\,$ m.

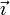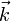3) Formar junto a los vectores $\,\vec{\imath}\,\,$ m y $\,\vec{k}\,$ m un paralelepípedo de volumen igual a 6 m³

2 Solución

Exigiremos a un vector genérico 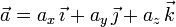$\vec{a}=a_x\,\vec{\imath}+a_y\,\vec{\jmath}+a_z\,\vec{k}\,$ las tres condiciones dadas. Por comodidad, prescindiremos de las unidades hasta llegar a la solución final (son todas unidades del SI).

La longitud de un vector es su módulo. Así que el cuadrado del módulo de $\vec{a}$ debe ser:

$a_x^2+a_y^2+a_z^2=(14)^2=196\,\,\,\,\,\,\,\, (1)$

La condición de ortogonalidad entre dos vectores viene dada por la nulidad de su producto escalar:

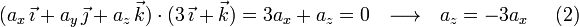
$(a_x\,\vec{\imath}+a_y\,\vec{\jmath}+a_z\,\vec{k})\cdot(3\,\vec{\imath}+\vec{k})=3a_x+a_z=0\,\,\,\,\longrightarrow\,\,\,\, a_z=-3a_x\,\,\,\,\,\,\,\, (2)$

El volumen del paralelepípedo que tiene a tres vectores por aristas es igual al valor absoluto de su producto mixto:

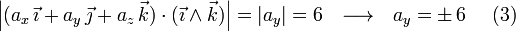
$\left|(a_x\,\vec{\imath}+a_y\,\vec{\jmath}+a_z\,\vec{k})\cdot(\vec{\imath}\wedge\vec{k})\right|=|a_y|=6\,\,\,\,\longrightarrow\,\,\,\, a_y=\pm\, 6\,\,\,\,\,\,\,\, (3)$

Sustituyendo (2) y (3) en (1) y resolviendo la ecuación resultante, se obtienen dos soluciones para 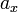$a_x\,$ . Y a cada una de esas dos soluciones de 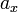$a_x\,$ le corresponde mediante (2) una solución en $a_z\,$ :

$a_x^2+36+9a_x^2=196\,\,\,\,\longrightarrow\,\,\,\,10\,a_x^2=160\,\,\,\,\longrightarrow\,\,\,\,a_x^2=16\,\,\,\,\longrightarrow\,\,\,\,\left\{ \begin{array}{l} a_x= 4 \,\,\,\,\longrightarrow\,\,\,\, a_z=-12 \\ a_x= -4 \,\,\,\,\longrightarrow\,\,\,\, a_z=12\end{array}\right.$

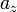Atendiendo a la duplicidad de signo en la solución obtenida para la componente $a_y\,$ en (3), podemos finalmente concluir que existen cuatro vectores que satisfacen las tres condiciones dadas, a saber:

$(4\,\vec{\imath}+6\,\vec{\jmath}-12\,\vec{k})\,\,\mathrm{m}\,\,;\,\,\,\,\,\,\,\,\,\, (4\,\vec{\imath}-6\,\vec{\jmath}-12\,\vec{k})\,\,\mathrm{m}\,\,;\,\,\,\,\,\,\,\,\,\, (-4\,\vec{\imath}+6\,\vec{\jmath}+12\,\vec{k})\,\,\mathrm{m}\,\,;\,\,\,\,\,\,\,\,\,\, (-4\,\vec{\imath}-6\,\vec{\jmath}+12\,\vec{k})\,\,\mathrm{m}$

1.11. Vectores con tres condiciones (Ex.Nov/11)

De Laplace

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES