Equilibrio de una tabla
De Laplace
Contenido |
1 Enunciado
Se tiene una plataforma de masa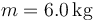 
y longitud 
(estando la masa distribuida uniformemente) que se apoya horizontalmente sobre dos caballetes de forma que los puntos de apoyo A y B están a 60 cm y 20 cm del centro C de la tabla, respectivamente.
- Calcule la fuerza que cada caballete ejerce sobre la tabla.
- Halle el valor máximo de la masa que se puede apoyar en el borde izquierdo de la plataforma si no se quiere que esta vuelque.
- Suponga que sobre el extremo derecho de la plataforma se apoya una masa de 2.2 kg. ¿Volcará la tabla? Si es así, determine la aceleración angular que adquiere la tabla el comenzar a girar en torno al punto de apoyo, así como la fuerza que ejerce ese caballete sobre la mesa en el instante en que empieza a volcar.
Tómese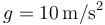 
.
Dato: Momento de inercia de una barra de masa m y longitud L respecto a un eje perpendicular a ella y que pasa por su centro: I = mL2; / 12.
2 Fuerzas en equilibrio
La plataforma constituye un sólido rígido. Cuando se encyentra en equilibrio deben cumplirse las dos condiciones
siendo los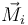 
los momentos de las fuerzas respecto a un punto cualquiera de la tabla. Por comodidad, tomaremos como punto de referencia el centro de la tabla, que también es su centro de masas.
Sobre la plataforma actúan tres fuerzas
- El peso
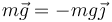
- La reacción del caballete de la izquierda
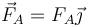
- La reacción del caballete de la derecha
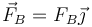
Puesto que las tres fuerzas van en el mismo sentido, la condición de equilibrio de fuerzas se reduce a una escalar
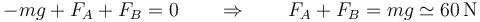
Con esta ecuación no nos basta para determinar las dos reacciones. Además necesitamos la anulación de sus momentos.
El momento de una fuerza aplicada en un punto P respecto a un punto fijo O lo da el producto vectorial
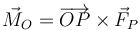
En nuestro caso, empleando el punto C como referencia tenemos la condición de equilibrio
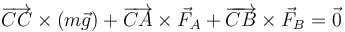
Desarrollando los vectores
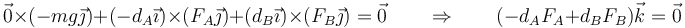
Se puede calcular el valor de estos sin necesidad de recurrir al producto vectorial (aunque obviamente, también puede hacerse con él). El momento de una fuerza en el caso de fuerzas paralelas es igual al producto de la fuerza por su brazo, y con un signo que indica si produce un giro antihorario (+) u horario (-).
Respecto al punto C, el peso, que está aplicado en él, no produce giro alguno y su momento es 0.
La reacción del caballete izquierdo produciría un giro en sentido horario, mientras que el del caballete derecho lo haría en sentido antihorario. Esto nos da la condición
Empleando productos vectoriales hubiera sido
