Solución de la 1ª convocatoria 12/13 (1ª parte)(GIE)

De Laplace

Revisión a fecha de 23:09 20 jun 2013; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Pregunta T.1
- 1.1 Solución
2 Preguntas T.2 y T.3
- 2.1 Pregunta T.2
  - 2.1.1 Solución
- 2.2 Pregunta T.3
  - 2.2.1 Solución
3 Pregunta T.4
- 3.1 Solución
4 Pregunta T.5
- 4.1 Solución
5 Pregunta T.6
- 5.1 Solución
6 Preguntas T.7 y T.8
- 6.1 Pregunta T.7
  - 6.1.1 Solución
- 6.2 Pregunta T.8
  - 6.2.1 Solución

1 Pregunta T.1

Un franklin es una unidad de carga eléctrica definida como aquella tal que dos cargas de 1 franklin situadas a 1 cm se ejercen una fuerza de 1 dina (=10⁻⁴N). ¿A cuantos culombios equivale un franklin?

1.11×10⁻¹⁹C
3.3 nC
0.33 nC
1.11×10⁻¹⁷C

1.1 Solución

Esta es una simple aplicación de la ley de Coulomb. La fuerza entre dos cargas iguales es, en módulo,

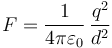
$F = \frac{1}{4\pi\varepsilon_0}\,\frac{q^2}{d^2}$

En este caso, empleando unidades del SI

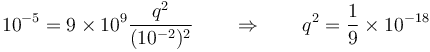
$10^{-5}=9\times 10^9\frac{q^2}{(10^{-2})^2} \qquad\Rightarrow\qquad q^2 = \frac{1}{9}\times 10^{-18}$

Tomando la raíz cuadrada

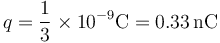
$q=\frac{1}{3}\times 10^{-9}\mathrm{C}=0.33\,\mathrm{nC}$

La respuesta correcta es por tanto la C.

2 Preguntas T.2 y T.3

2.1 Pregunta T.2

Se tienen dos superficies conductoras esféricas concéntricas, de radios 1 cm y 3 cm, respectivamente. Inicialmente la interior (1) almacena una carga de −40 nC y la exterior (2) una de +20 nC.

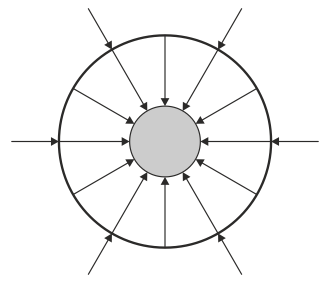
¿Cuál de las siguientes figuras describe adecuadamente el campo eléctrico en el sistema?

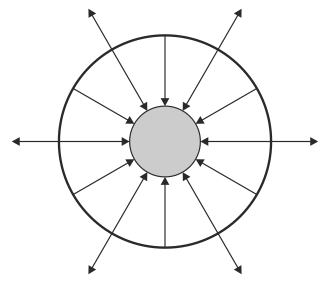
A	B


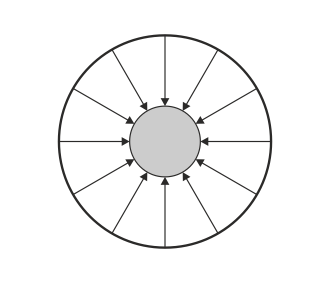
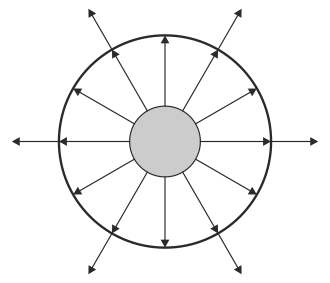
C	D

2.1.1 Solución

La solución a esta cuestión nos la da la ley de Gauss.

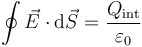
$\oint \vec{E}\cdot\mathrm{d}\vec{S}=\frac{Q_\mathrm{int}}{\varepsilon_0}$

Esta nos dice que una superficie cerrada envuelve una carga neta positiva, el flujo del campo eléctrico será positivo, es decir, el campo va hacia afuera, mientras que si envolvemos a una carga neta negativa, el flujo será negativo, esto es, el campo irá hacia adentro.

Si consideramos una superficie esférica de radio entre 1 y 3cm, es decir, entre los dos conductores, envolvemos solo la carga de la esfera 1, que es

$Q_\mathrm{int}=Q_1 = -40\,\mathrm{nC}< 0$

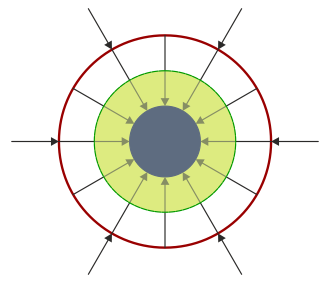
Por tanto el flujo en esta superficie es negativo, y el campo irá hacia adentro.

Si ahora consideramos una superficie de radio mayor que 3cm, es decir, exterior a las dos esferas, la carga encerrada es la de las dos

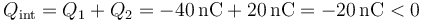
$Q_\mathrm{int}=Q_1+Q_2 = -40\,\mathrm{nC} + 20\,\mathrm{nC}=-20\,\mathrm{nC} < 0$

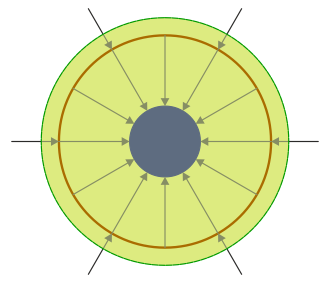
Al ser también negativo, quiere decir que en el exterior el campo irá igualmente hacia adentro.

Por tanto la respuesta correcta es la B.

2.2 Pregunta T.3

Se conectan las dos esferas por un cable. Una vez que se alcanza el equilibrio electrostático, ¿cómo queda el reparto de cargas entre las dos?

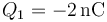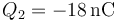
$Q_1=-2\,\mathrm{nC}$ , $Q_2 = -18\,\mathrm{nC}$
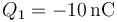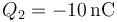
$Q_1=-10\,\mathrm{nC}$ , $Q_2 = -10\,\mathrm{nC}$
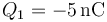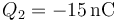
$Q_1=-5\,\mathrm{nC}$ , $Q_2 = -15\,\mathrm{nC}$
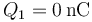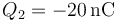
$Q_1=0\,\mathrm{nC}$ , $Q_2 = -20\,\mathrm{nC}$

2.2.1 Solución

Cuando los dos conductores se unen por un cable pasan a formar un solo conductor. Este único conductor tiene un huecos en su interior, pero en este espacio está completamente vacío. Entonces, se comporta como una jaula de Faraday vacía: el campo en el hueco es nulo. Si el campo en el hueco es nulo, su flujo es una superficie intermedia como la de antes y por tanto la carga del conductor es nula

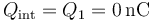
$Q_\mathrm{int}=Q_1 = 0\,\mathrm{nC}$

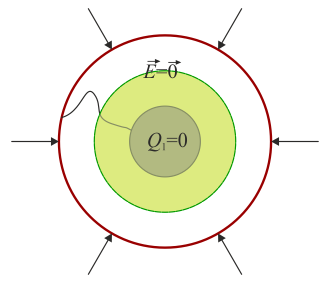
Toda la carga del conductor está en su superficie exterior, que es la cara de fuera

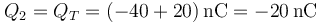
$Q_2 = Q_T = (-40+20)\,\mathrm{nC}=-20\,\mathrm{nC}$

Por tanto la respuesta correcta es la D.

Otra forma equivalente de verlo es que si los dos conductores están al mismo potencial, por estar unidos por un cable, no puede haber líneas de campo que vayan de una esfera a la otra, por lo que el campo entre ellas es nulo.

Y otra forma más es considerar que la repulsión culombiana intenta alejar las cargas lo más posibles, por lo que las cargas negativas de la esfera interior se alejan yéndose al exterior (donde además son atraídas por las positivas).

3 Pregunta T.4

Tres placas conductoras circulares de radio 12 cm se encuentran situadas paralelamente con una distancia de 1 mm entre ellas. El espacio intermedio está vacío. La placa central se encuentra a un potencial de 100\,V, mientras que las exteriores están puestas a tierra.

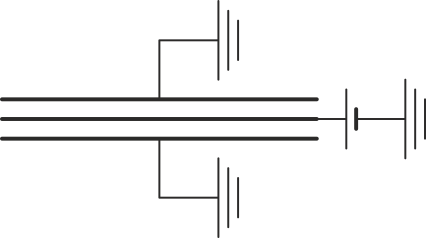
La energía electrostática almacenada en el sistema vale…

8μJ
4μJ
2μJ
1μJ

3.1 Solución

Este sistema equivale a dos condensadores puestos en paralelo,

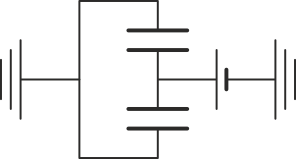
por lo que la energía almacenada en el sistema es

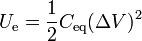
$U_\mathrm{e}=\frac{1}{2}C_\mathrm{eq}(\Delta V)^2$

siendo la capacidad equivalente de la asociación

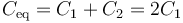
$C_\mathrm{eq} = C_1 + C_2 = 2C_1\,$

La capacidad de cada condensador es

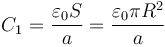
$C_1 = \frac{\varepsilon_0 S}{a}=\frac{\varepsilon_0 \pi R^2}{a}$

Sustituyendo los valores numéricos y aplicando que

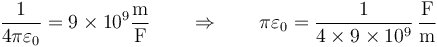
$\frac{1}{4\pi\varepsilon_0}=9\times 10^9\frac{\mathrm{m}}{\mathrm{F}}\qquad\Rightarrow\qquad \pi\varepsilon_0 = \frac{1}{4\times 9\times 10^9}\,\frac{\mathrm{F}}{\mathrm{m}}$

obtenemos la capacidad individual

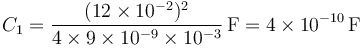
$C_1 = \frac{(12\times 10^{-2})^2}{4\times 9\times 10^{-9}\times 10^{-3}}\,\mathrm{F}=4\times 10^{-10}\,\mathrm{F}$

y la de la asociación

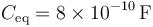
$C_\mathrm{eq}= 8\times 10^{-10}\,\mathrm{F}$

Finalmente la energía almacenada vale

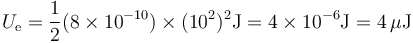
$U_\mathrm{e} = \frac{1}{2}(8\times 10^{-10})\times(10^2)^2 \mathrm{J}= 4\times10^{-6}\mathrm{J}=4\,\mu\mathrm{J}$

Por tanto la respuesta correcta es la B.

4 Pregunta T.5

Un circuito real está formado por una pila, que se conecta por sendos cables a las placas de un condensador real, en cuyo interior hay un dieléctrico con permitividad y conductividad no nulas.

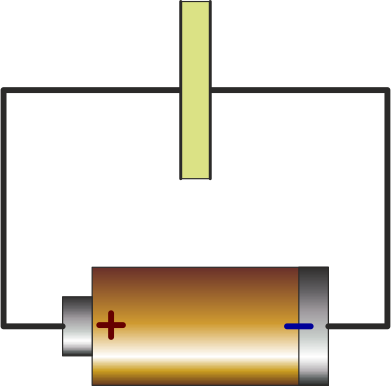
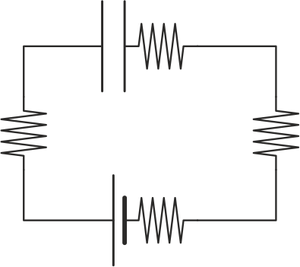
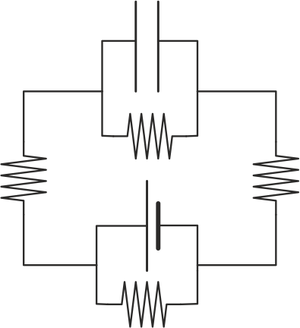
¿Cómo es el circuito equivalente de este sistema?

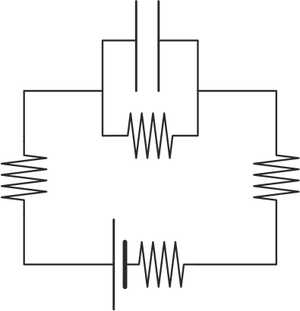
A	B


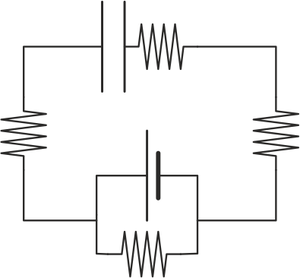
C	D

4.1 Solución

Sabemos que:

Cada cable de conexión es equivalente a una resistencia eléctrica, por tratarse de un hilo de material conductor.

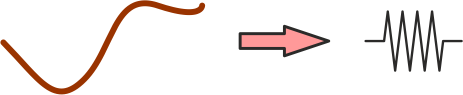
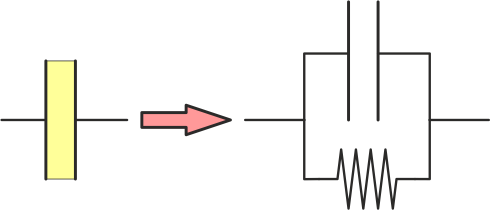
Un condensador real equivale a un condensador ideal y a una resistencia puestos en paralelo

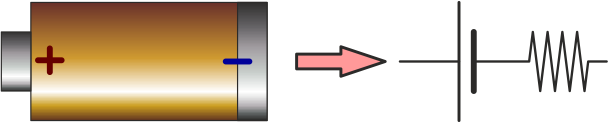
Una fuente de tensión real equivale a una fuente ideal y una resistencia puestas en serie

por tanto, la combinación de estos tres modelos nos dice que la respuesta correcta es la A

5 Pregunta T.6

Dos espiras circulares se sitúan de la manera indicada en la figura, con las intensidades de corriente en los sentidos que se indican. ¿Cómo es la interacción de la inferior sobre la superior?

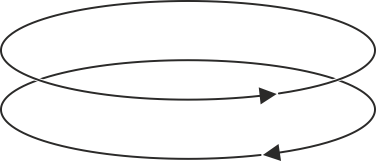
La atrae.
La repele.
No ejerce ninguna interacción
Aparece un par de fuerzas que tiende a darle la vuelta.

5.1 Solución

Cuando se aplica la ley de Lorentz para la fuerza entre cargas en movimiento o entre dos hilos de corriente, se obtiene la regla general:

Corrientes paralelas (↑↑) se atraen.
Corrientes antiparalelas (↑↓) se repelen.

Como en este caso, tenemos corrientes antiparalelas, el efecto es de repulsión y la respuesta correcta es la B.

6 Preguntas T.7 y T.8

6.1 Pregunta T.7

Una espira en forma de escuadra con resistencia $R$ y autoinducción despreciable penetra en un campo magnético uniforme con una velocidad paralela a uno de sus catetos.

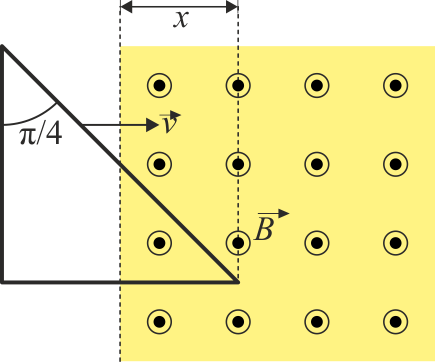
Si la velocidad de la espira es constante, ¿como es la corriente que se induce en ella mientras va entrando?

Aumenta cuadráticamente con el tiempo.
Tiende exponencialmente a un valor constante
Permanece constante
Aumenta linealmente con el tiempo.

6.1.1 Solución

De acuerdo con la ley de Faraday y la ley de Ohm, la corriente que circula por la espira cumple

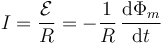
$I = \frac{\mathcal{E}}{R}=-\frac{1}{R}\,\frac{\mathrm{d}\Phi_m}{\mathrm{d}t}$

El cálculo es análogo al de una espira cuadrada solo que en este caso la superficie donde hay campo magnético es un triángulo, por lo que

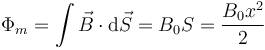
$\Phi_m = \int \vec{B}\cdot\mathrm{d}\vec{S}=B_0S = \frac{B_0 x^2}{2}$

ya que el área es la de un triángulo de base $x$ y altura también $x$ (por ser una escuadra. Puesto que la espira se mueve uniformemente

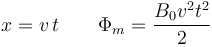
$x = v\,t\qquad\Phi_m = \frac{B_0 v^2 t^2}{2}$

Derivando esto respecto al tiempo obtenemos

$I = -\frac{B_0 v^2 t}{R}=K t$

luego el valor de la intensidad de corriente aumenta linealmente con el tiempo y la respuesta correcta es la D.

6.2 Pregunta T.8

¿Y la fuerza magnética sobre la espira?

Aumenta cuadráticamente con el tiempo.
Tiende exponencialmente a un valor constante
Permanece constante
Aumenta linealmente con el tiempo.

6.2.1 Solución

La fuerza sobre una espira inmersa parcialmente es un campo uniforme la da la expresión

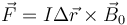
$\vec{F} = I \Delta\vec{r}\times\vec{B}_0$

siendo

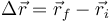
$\Delta \vec{r}=\vec{r}_f-\vec{r}_i$

el vector que va del punto donde la espira penetra en el campo y el punto por el que sale. En este caso

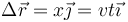
$\Delta \vec{r}=x\vec{\jmath}=v t\vec{\imath}$

Es decir, la corriente aumenta linealmente con el tiempo y la longitud de la corriente también lo hace, por lo que la fuerza, producto de las dos, aumentará cuadráticamente con el tiempo

$\vec{F}=(K t)(v t\vec{\jmath})\times(B_0\vec{k}) = (K v B_0\vec{\imath}) t^2=\vec{C} t^2$

Por tanto, la respuesta correcta es la A.