Solución de la 1ª convocatoria 12/13 (1ª parte)(GIE)
De Laplace
Contenido |
1 Pregunta T.1
Un franklin es una unidad de carga eléctrica definida como aquella tal que dos cargas de 1 franklin situadas a 1 cm se ejercen una fuerza de 1 dina (=10−4N). ¿A cuantos culombios equivale un franklin?
- 1.11×10−19C
- 0.33 nC
- 3.3 nC
- 1.11×10−17C
1.1 Solución
Esta es una simple aplicación de la ley de Coulomb. La fuerza entre dos cargas iguales es, en módulo,
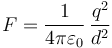
En este caso, empleando unidades del SI
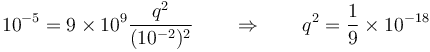
Tomando la raíz cuadrada
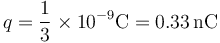
La respuesta correcta es por tanto la B.
2 Preguntas T.2 y T.3
2.1 Pregunta T.2
Se tienen dos superficies conductoras esféricas concéntricas, de radios 1 cm y 3 cm, respectivamente. Inicialmente la interior (1) almacena una carga de −40 nC y la exterior (2) una de +20 nC.
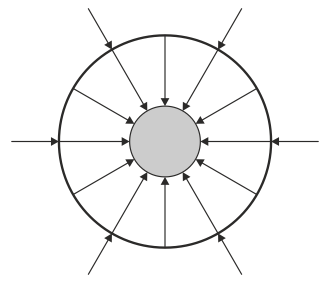
¿Cuál de las siguientes figuras describe adecuadamente el campo eléctrico en el sistema?
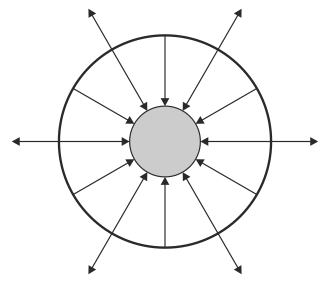
| 
|
| A | B |
|---|---|
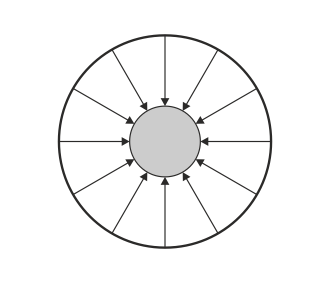
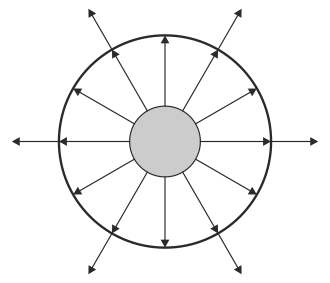
| 
|
| C | D |
2.1.1 Solución
La solución a esta cuestión nos la da la ley de Gauss.
\oint \vec{E}\cdot\mathrm{d}\vec{S}=\frac{Q_\mathrm{int}}{\varepsilon_0} Esta nos dice que una superficie cerrada envuelve una carga neta positiva, el flujo del campo eléctrico será positivo, es decir, el campo va hacia afuera, mientras que si envolvemos a una carga neta negativa, el flujo será negativo, esto es, el campo irá hacia adentro.
Si consideramos una superficie esférica de radio entre 1 y 3cm, es decir, entre los dos conductores, envolvemos solo la carga de la esfera 1, que es

Por tanto el flujo en esta superficie es negativo, y el campo irá hacia adentro.
Si ahora consideramos una superficie de radio mayor que 3cm, es decir, exterior a las dos esferas, la carga encerrada es la de las dos
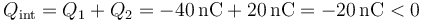
Al ser también negativo, quiere decir que en el exterior el campo irá igualmente hacia adentro.
Por tanto la respuesta correcta es la B.





